【题目】2016年一交警统计了某段路过往车辆的车速大小与发生的交通事故次数,得到如下表所示的数据:
车速 |
|
|
|
|
|
事故次数 |
|
|
|
|
|
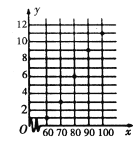
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测2017年该路段路况及相关安全设施等不变的情况下,车速达到![]() 时,可能发生的交通事故次数.
时,可能发生的交通事故次数.
(参考数据:![]() )
)
[参考公式: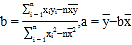 ]
]

参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 次.
次.
【解析】分析:(1)概率表中数据画出散点图;
(2)求出![]() 由已知可得
由已知可得![]() 代入公式可求
代入公式可求![]() ,
,
从而得到![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)将![]() 代入线性回归方程.即可预测2017年该路段路况及相关安全设施等不变的情况下,车速达到
代入线性回归方程.即可预测2017年该路段路况及相关安全设施等不变的情况下,车速达到![]() 时,可能发生的交通事故次数.
时,可能发生的交通事故次数.
详解:
(1)散点图如图所示
(2)由已知可得![]()
所以,由最小二乘法确定的回归方程的系数为![]() ,
,
![]()
因此,所求的线性回归方程为![]()
(3)由线性回归方程,知当![]() 时,
时,![]() .
.
所以在年该路段路况及相关安全设施等不变的情况下,车速达到![]() 时,可能发生的交通事故次数为
时,可能发生的交通事故次数为![]() 次.
次.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,函数
,函数 的最小值为
的最小值为 .
.(1)当
 时,求
时,求 的值;
的值;(2)求
 ;
;(3)已知函数
 为定义在上的增函数,且对任意的
为定义在上的增函数,且对任意的 都满足
都满足 ,问:是否存在这样的实数
,问:是否存在这样的实数 ,使不等式
,使不等式 对所有
对所有 恒成立,若存在,求出
恒成立,若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图如图所示,且该几何体的体积是3,则正视图的
 的值__________.
的值__________.
【答案】3
【解析】 由已知中的三视图可得该几何体是一个以直角梯形为底面,梯形上下边长为
 和
和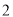 ,高为
,高为 ,
,如图所示,
 平面
平面 ,
,所以底面积为
 ,
,几何体的高为
 ,所以其体积为
,所以其体积为 .
.
点睛:在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何体实际形状时,一般是以正视图和俯视图为主,结合侧视图进行综合考虑.求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解.
【题型】填空题
【结束】
16【题目】已知椭圆
 :
:  的右焦点为
的右焦点为 ,
,  为直线
为直线 上一点,线段
上一点,线段 交
交 于点
于点 ,若
,若 ,则
,则 __________.
__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出如下结论:
①函数
 是奇函数;
是奇函数;②存在实数
 ,使得
,使得 ;
;③若
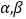 是第一象限角且
是第一象限角且 ,则
,则 ;
;④
 是函数
是函数 的一条对称轴方程;
的一条对称轴方程;⑤函数
 的图形关于点
的图形关于点 成中心对称图形.
成中心对称图形.其中正确的结论的序号是__________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校从参加高一年级期中考试的学生中抽出
 名学生,并统计了她们的数学成绩(成绩均为整数且满分为
名学生,并统计了她们的数学成绩(成绩均为整数且满分为 分),数学成绩分组及各组频数如下:
分),数学成绩分组及各组频数如下:
样本频率分布表:
分组
频数
频率

















合计


(1)在给出的样本频率分布表中,求
 的值;
的值;(2)估计成绩在
 分以上(含
分以上(含 分)学生的比例;
分)学生的比例;(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在
 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在 中的某一位同学.已知甲同学的成绩为
中的某一位同学.已知甲同学的成绩为 分,乙同学的成绩为
分,乙同学的成绩为 分,求甲、乙两同学恰好被安排在同一小组的概率.
分,求甲、乙两同学恰好被安排在同一小组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公园摩天轮的半径为
 ,圆心距地面的高度为
,圆心距地面的高度为 ,摩天轮做匀速转动,每
,摩天轮做匀速转动,每 转一圈,摩天轮上的点
转一圈,摩天轮上的点 的起始位置在最低点处.
的起始位置在最低点处.(1)已知在时刻
 时
时 距离地面的高度
距离地面的高度 ,(其中
,(其中 ),求
),求 时
时 距离地面的高度;
距离地面的高度;(2)当离地面
 以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?
以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,函数
,函数 的最小值为
的最小值为 .
.(1)当
 时,求
时,求 的值;
的值;(2)求
 ;
;(3)已知函数
 为定义在上的增函数,且对任意的
为定义在上的增函数,且对任意的 都满足
都满足 ,问:是否存在这样的实数
,问:是否存在这样的实数 ,使不等式
,使不等式 对所有
对所有 恒成立,若存在,求出
恒成立,若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
相关试题

