【题目】【2017届河北省衡水中学高三上学期六调】已知函数![]() ,其中
,其中![]() 均为实数,
均为实数,![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的极值;
的极值;
(2)设![]() ,若对任意的
,若对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由题对![]() 得
得![]() ,研究其单调性,可得当
,研究其单调性,可得当![]()
![]()
![]()
(2)由题当![]()
![]()
![]()
![]()
![]() ,构造函数
,构造函数![]() ,
,
由单调性可得![]()
![]()
![]() ,
,
则![]() 等价于
等价于![]() ,
,
即![]() ,
,
故又构造函数![]() ,
,
可知![]()
![]()
![]() 在区间
在区间![]()
即![]() 在区间
在区间![]()
∴![]() ,设
,设![]()
则![]() ,
,
∵![]() ,
,
∴![]() ,则
,则![]()
![]()
∴![]()
![]()
![]() ,∴
,∴![]() ,
,
试题解析:(1)由题得,![]() ,
,
令![]() ,得
,得![]()
列表如下:
|
| 1 |
|
| 大于0 | 0 | 小于0 |
|
| 极大值 |
|
∴当![]()
![]()
![]()
(2)当![]()
![]()
∵![]() 在区间
在区间![]()
∴![]()
![]()
设![]() ,
,
∵![]() 在区间
在区间![]()
∴![]()
![]()
![]() ,
,
则![]() 等价于
等价于![]() ,
,
即![]() ,
,
设![]() ,
,
则![]()
![]()
∴![]() 在区间
在区间![]()
∴![]() 在区间
在区间![]()
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,则
,则![]()
![]()
∴![]()
![]()
![]() ,∴
,∴![]() ,
,
∴实数![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
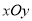 中,已知曲线
中,已知曲线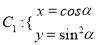 (
(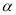 为参数),在以
为参数),在以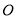 为极点,
为极点, 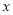 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线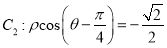 ,曲线
,曲线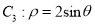 .
.(1)求曲线
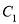 与
与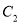 的交点
的交点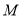 的直角坐标;
的直角坐标;(2)设点
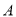 ,
, 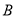 分别为曲线
分别为曲线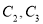 上的动点,求
上的动点,求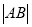 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式的值:
(1)2log32-log3
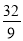 +log38-5
+log38-5 ;
;(2)[(1-log63)2+log62·log618]÷log64.
-
科目: 来源: 题型:
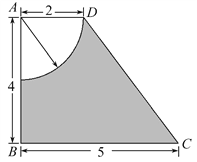
查看答案和解析>>【题目】如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD-A1B1C1D1中,P,M,N分别为棱DD1,AB,BC的中点.
(1)求二面角B1-MN-B的正切值.
(2)求证:PB⊥平面MNB1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本,对高一年级的100名学生的成绩进行统计,并按
 ,
,  ,
,  ,
,  ,
,  ,
,  分组,得到成绩分布的频率分布直方图(如图)。
分组,得到成绩分布的频率分布直方图(如图)。
(1)若规定60分以上(包括60分)为合格,计算高一年级这次竞赛的合格率;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
(3)若高二年级这次竞赛的合格率为
 ,由以上统计数据填写下面
,由以上统计数据填写下面 列联表,并问是否有
列联表,并问是否有 的把握认为“这次知识竞赛的成绩与年级有关”。
的把握认为“这次知识竞赛的成绩与年级有关”。高一
高二
合计
合格人数
不合格人数
合计
 附:参考数据与公式
附:参考数据与公式高一
高二 合计
合格人数
a
b
a+b
不合格人数
c
d
c+d
合计
a+c
b+d
n

0.050
0.010
0.001

3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l经过两直线l1:2x-y+4=0与l2:x-y+5=0的交点,且与直线x-2y-6=0垂直.
(1)求直线l的方程.
(2)若点P(a,1)到直线l的距离为
 ,求实数a的值.
,求实数a的值.
相关试题

