【题目】已知正项数列{an}的前n项和为Sn , 数列{an}满足,2Sn=an(an+1).
(1)求数列{an}的通项公式;
(2)设数列{ ![]() }的前n项和为An , 求证:对任意正整数n,都有An<
}的前n项和为An , 求证:对任意正整数n,都有An< ![]() 成立;
成立;
(3)数列{bn}满足bn=( ![]() )nan , 它的前n项和为Tn , 若存在正整数n,使得不等式(﹣2)n﹣1λ<Tn+
)nan , 它的前n项和为Tn , 若存在正整数n,使得不等式(﹣2)n﹣1λ<Tn+ ![]() ﹣2n﹣1成立,求实数λ的取值范围.
﹣2n﹣1成立,求实数λ的取值范围.
参考答案:
【答案】
(1)解: ![]() ,当n≥2时,
,当n≥2时, ![]() ,
,
两式相减得: ![]() ,所以(an+an﹣1)(an﹣an﹣1﹣1)=0.
,所以(an+an﹣1)(an﹣an﹣1﹣1)=0.
因为数列{an}为正项数列,故an+an﹣1≠0,也即an﹣an﹣1=1,
所以数列{an}为以1为首项1为公差的等差数列,故通项公式为an=n,n∈N*
(2)解: ![]()
![]() =
= ![]() ,
,
所以对任意正整数n,都有 ![]() 成立
成立
(3)解:易知 ![]() ,则
,则 ![]() ,①,
,①,
![]() ,②
,②
①﹣②可得: ![]() .
.
故 ![]() ,所以不等式
,所以不等式 ![]() 成立,
成立,
若n为偶数,则 ![]() ,所以
,所以 ![]() .
.
设 ![]() ,则y=﹣2t+t2+1=(t﹣1)2在
,则y=﹣2t+t2+1=(t﹣1)2在 ![]() 单调递减,
单调递减,
故当 ![]() 时,
时, ![]() ,所以
,所以 ![]() ;
;
若n为奇数,则 ![]() ,所以
,所以 ![]() .
.
设 ![]() ,则y=2t﹣t2﹣1=﹣(t﹣1)2在(0,1]单调递增,
,则y=2t﹣t2﹣1=﹣(t﹣1)2在(0,1]单调递增,
故当t=1时,ymax=0,所以λ<0.
综上所述,λ的取值范围λ<0或 ![]()
【解析】(1)根据数列的递推公式即可求出数列{an}的通项公式,(2) ![]() =
= ![]() <
< ![]() =
= ![]() ﹣
﹣ ![]() ,利用放缩法即可证明,(3)先利用错位相减法求出数列{bn}的前n项和为Tn , 不等式(﹣2)n﹣1λ<Tn+
,利用放缩法即可证明,(3)先利用错位相减法求出数列{bn}的前n项和为Tn , 不等式(﹣2)n﹣1λ<Tn+ ![]() ﹣2n﹣1成立,转化为
﹣2n﹣1成立,转化为 ![]() 成立,分n为偶数和奇数,根据函数的性质即可求出实数λ的取值范围
成立,分n为偶数和奇数,根据函数的性质即可求出实数λ的取值范围
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系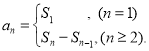 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】是否存在一个等比数列{an}同时满足下列三个条件:①a1+a6=11且a3a4=
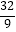 ;②an+1>an(n∈N*);③至少存在一个m(m∈N*且m>4),使得
;②an+1>an(n∈N*);③至少存在一个m(m∈N*且m>4),使得  am﹣1 , am2 , am+1+
am﹣1 , am2 , am+1+  依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
依次构成等差数列?若存在,求出通项公式;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
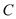 的两个焦点是
的两个焦点是 和
和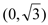 ,并且经过点
,并且经过点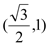 ,抛物线
,抛物线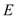 的顶点在坐标原点,焦点恰好是椭圆
的顶点在坐标原点,焦点恰好是椭圆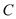 的右顶点.
的右顶点.(Ⅰ)求椭圆
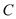 和抛物线
和抛物线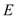 的标准方程;
的标准方程;(Ⅱ)已知点
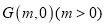 为抛物线
为抛物线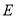 内一个定点,过
内一个定点,过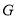 作斜率分别为
作斜率分别为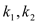 的两条直线交抛物线
的两条直线交抛物线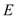 于点
于点 ,且
,且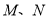 分别是
分别是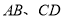 的中点,若
的中点,若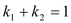 ,求证:直线
,求证:直线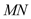 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知
 ,且
,且 .
.(1)求
 的最小值;
的最小值;(2)求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某校高三上学期期末数学考试成绩中,随机抽取了
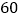 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图: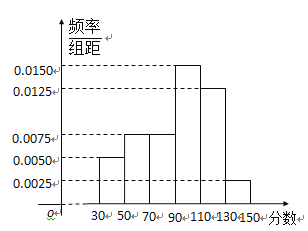
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在
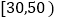 和
和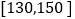 的学生中共抽取
的学生中共抽取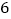 人,该
人,该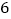 人中成绩在
人中成绩在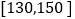 的有几人?
的有几人?(3)在(2)中抽取的
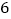 人中,随机抽取
人中,随机抽取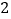 人,求分数在
人,求分数在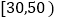 和
和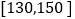 各
各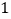 人的概率.
人的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 )的部分图象如图所示,若将f(x)的图象上所有点向右平移
)的部分图象如图所示,若将f(x)的图象上所有点向右平移  个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( ) 
A. ,k∈Z
,k∈Z
B. ,k∈Z
,k∈Z
C. ,k∈Z
,k∈Z
D. ,k∈Z
,k∈Z -
科目: 来源: 题型:
查看答案和解析>>【题目】以下关于命题的说法正确的有(选择所有正确命题的序号).
(1)“若
 ,则函数
,则函数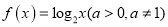 在其定义域内是减函数”是真命题;
在其定义域内是减函数”是真命题;(2)命题“若
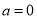 ,则
,则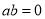 ”的否命题是“若
”的否命题是“若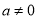 ,则
,则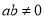 ”;
”;(3)命题“若
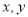 都是偶函数,则
都是偶函数,则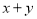 也是偶数”的逆命题为真命题;
也是偶数”的逆命题为真命题;(4)命题“若
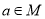 ,则
,则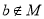 ”与命题“若
”与命题“若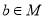 ,则
,则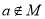 ”等价.
”等价.A. (1)(3) B. (2)(3) C. (2)(4) D. (3)(4)
相关试题

