【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,若将f(x)的图象上所有点向右平移
)的部分图象如图所示,若将f(x)的图象上所有点向右平移 ![]() 个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( ) 
A.![]() ,k∈Z
,k∈Z
B.![]() ,k∈Z
,k∈Z
C.![]() ,k∈Z
,k∈Z
D.![]() ,k∈Z
,k∈Z
参考答案:
【答案】A
【解析】解:由图可知A=2,T=4( ![]() ﹣
﹣ ![]() )=π, ∴=
)=π, ∴= ![]() =2.
=2.
∵由图可得点( ![]() ,2)在函数图象上,可得:2sin(2×
,2)在函数图象上,可得:2sin(2× ![]() +φ)=2,解得:2×
+φ)=2,解得:2× ![]() +φ=2kπ+
+φ=2kπ+ ![]() ,k∈Z,
,k∈Z,
∴由|φ|< ![]() ,可得:φ=
,可得:φ= ![]() ,
,
∴f(x)=2sin(2x+ ![]() ).
).
∵若将y=f(x)的图象向右平移 ![]() 个单位后,得到的函数解析式为:g(x)=2sin[2(x﹣
个单位后,得到的函数解析式为:g(x)=2sin[2(x﹣ ![]() )+
)+ ![]() ]=2sin(2x+
]=2sin(2x+ ![]() ).
).
∴由2kπ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,可得kπ﹣
,k∈Z,可得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
∴函数g(x)的单调增区间为:[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z.
],k∈Z.
故选:A.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数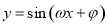 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知
 ,且
,且 .
.(1)求
 的最小值;
的最小值;(2)求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项数列{an}的前n项和为Sn , 数列{an}满足,2Sn=an(an+1).
(1)求数列{an}的通项公式;
(2)设数列{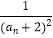 }的前n项和为An , 求证:对任意正整数n,都有An<
}的前n项和为An , 求证:对任意正整数n,都有An<  成立;
成立;
(3)数列{bn}满足bn=( )nan , 它的前n项和为Tn , 若存在正整数n,使得不等式(﹣2)n﹣1λ<Tn+
)nan , 它的前n项和为Tn , 若存在正整数n,使得不等式(﹣2)n﹣1λ<Tn+ 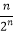 ﹣2n﹣1成立,求实数λ的取值范围.
﹣2n﹣1成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某校高三上学期期末数学考试成绩中,随机抽取了
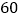 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图: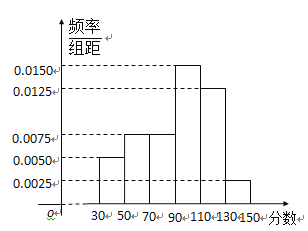
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在
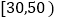 和
和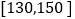 的学生中共抽取
的学生中共抽取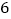 人,该
人,该 人中成绩在
人中成绩在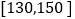 的有几人?
的有几人?(3)在(2)中抽取的
 人中,随机抽取
人中,随机抽取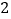 人,求分数在
人,求分数在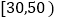 和
和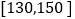 各
各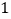 人的概率.
人的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下关于命题的说法正确的有(选择所有正确命题的序号).
(1)“若
 ,则函数
,则函数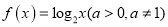 在其定义域内是减函数”是真命题;
在其定义域内是减函数”是真命题;(2)命题“若
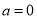 ,则
,则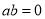 ”的否命题是“若
”的否命题是“若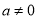 ,则
,则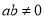 ”;
”;(3)命题“若
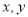 都是偶函数,则
都是偶函数,则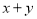 也是偶数”的逆命题为真命题;
也是偶数”的逆命题为真命题;(4)命题“若
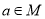 ,则
,则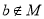 ”与命题“若
”与命题“若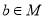 ,则
,则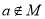 ”等价.
”等价.A. (1)(3) B. (2)(3) C. (2)(4) D. (3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
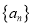 中,
中, 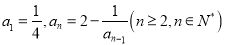 ,数列
,数列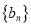 满足
满足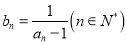 .
.(1)求证:数列
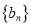 是等差数列,写出
是等差数列,写出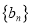 的通项公式;
的通项公式;(2)求数列
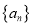 的通项公式及数列
的通项公式及数列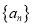 中的最大项与最小项.
中的最大项与最小项. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
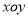 中,以坐标原点为极点,
中,以坐标原点为极点, 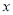 轴正半轴为极轴建立极坐标系,
轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:
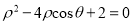 .
.(1)将极坐标方程化为直角坐标方程;
(2)若点
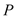
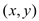 在该圆上,求
在该圆上,求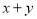 的最大值和最小值.
的最大值和最小值.
相关试题

