【题目】是否存在一个等比数列{an}同时满足下列三个条件:①a1+a6=11且a3a4= ![]() ;②an+1>an(n∈N*);③至少存在一个m(m∈N*且m>4),使得
;②an+1>an(n∈N*);③至少存在一个m(m∈N*且m>4),使得 ![]() am﹣1 , am2 , am+1+
am﹣1 , am2 , am+1+ ![]() 依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
参考答案:
【答案】解:假设存在等比数列{an}同时满足三个条件, 由①可得  ,
,
由②可知数列{an}是递增的,则a6>a1 ,
解上面方程组得  ,
,
设等比数列的公比q,则 ![]() ,q=2.
,q=2.
此时 ![]() .
.
由③可知 ![]()
![]() .
.
解得m=3,与已知m>4矛盾.
故这样的数列{an}不存在
【解析】假设存在等比数列{an}同时满足三个条件,由①②结合等比数列的性质求得a1、a6的值,从而求出等比数列的公比,得到等比数列的通项公式,结合 ![]() am﹣1 , am2 , am+1+
am﹣1 , am2 , am+1+ ![]() 成等差数列求出m的值为3,与m>4矛盾,说明假设错误.
成等差数列求出m的值为3,与m>4矛盾,说明假设错误.
【考点精析】关于本题考查的等差数列的性质,需要了解在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某金匠以黄金为原材料加工一种饰品,经多年的数据统计得知,该金匠平均每加5 个饰品中有4个成品和1个废品,每个成品可获利3万元,每个废品损失1万元,假设该金匠加工每件饰品互不影响,以频率估计概率.
(1)若金金匠加工4个饰品,求其中废品的数量不超过1的概率;
(2)若该金匠加工了 3个饰品,求他所获利润的数学期望.
(两小问的计算结果都用分数表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知在锐角△ABC中,角A,B,C所对的边分别为a,b,c,且tanC=
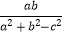 . (Ⅰ)求角C大小;
. (Ⅰ)求角C大小;
(Ⅱ)当c=1时,求ab的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
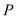 是圆
是圆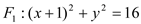 上任意一点,点
上任意一点,点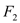 的坐标为
的坐标为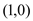 ,直线
,直线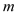 分别与线段
分别与线段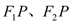 交于
交于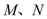 两点,且
两点,且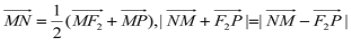 .
.(1)求点
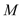 的轨迹
的轨迹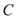 的方程;
的方程;(2)直线
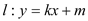 与轨迹
与轨迹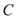 相交于
相交于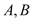 两点,设
两点,设 为坐标原点,
为坐标原点, 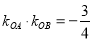 ,判断
,判断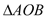 的面积是否为定值?若是,求出定值,若不是,说明理由.
的面积是否为定值?若是,求出定值,若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
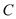 的两个焦点是
的两个焦点是 和
和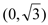 ,并且经过点
,并且经过点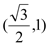 ,抛物线
,抛物线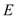 的顶点在坐标原点,焦点恰好是椭圆
的顶点在坐标原点,焦点恰好是椭圆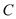 的右顶点.
的右顶点.(Ⅰ)求椭圆
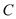 和抛物线
和抛物线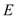 的标准方程;
的标准方程;(Ⅱ)已知点
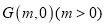 为抛物线
为抛物线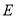 内一个定点,过
内一个定点,过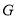 作斜率分别为
作斜率分别为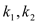 的两条直线交抛物线
的两条直线交抛物线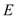 于点
于点 ,且
,且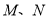 分别是
分别是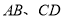 的中点,若
的中点,若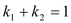 ,求证:直线
,求证:直线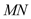 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知
 ,且
,且 .
.(1)求
 的最小值;
的最小值;(2)求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项数列{an}的前n项和为Sn , 数列{an}满足,2Sn=an(an+1).
(1)求数列{an}的通项公式;
(2)设数列{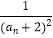 }的前n项和为An , 求证:对任意正整数n,都有An<
}的前n项和为An , 求证:对任意正整数n,都有An<  成立;
成立;
(3)数列{bn}满足bn=( )nan , 它的前n项和为Tn , 若存在正整数n,使得不等式(﹣2)n﹣1λ<Tn+
)nan , 它的前n项和为Tn , 若存在正整数n,使得不等式(﹣2)n﹣1λ<Tn+ 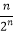 ﹣2n﹣1成立,求实数λ的取值范围.
﹣2n﹣1成立,求实数λ的取值范围.
相关试题

