【题目】下列命题正确的是( )
A.命题“x∈R,使得x2﹣1<0”的否定是:x∈R,均有x2﹣1<0
B.命题“若x=3,则x2﹣2x﹣3=0”的否命题是:若x≠3,则x2﹣2x﹣3≠0
C.“ ![]() ”是“
”是“ ![]() ”的必要而不充分条件
”的必要而不充分条件
D.命题“cosx=cosy,则x=y”的逆否命题是真命题
参考答案:
【答案】B
【解析】解:对于A,“x∈R,使得x2﹣1<0”的否定是:x∈R,均有x2﹣1≥0,命题A错误;
对于B,“若x=3,则x2﹣2x﹣3=0”的否命题是:若x≠3,则x2﹣2x﹣3≠0,命题B正确;
对于C, ![]() 时,
时, ![]() ,充分性成立;
,充分性成立;
![]() 时,α=kπ+
时,α=kπ+ ![]() 或α=kπ+
或α=kπ+ ![]() ,k∈Z,必要性不成立;
,k∈Z,必要性不成立;
是充分不必要条件,命题B错误;
对于D,命题“cosx=cosy,则x=y”是假命题,
则它的逆否命题也是假命题,∴命题D错误.
故选:B.
根据四种命题之间的关系,对每一个命题判断真假性即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
-
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ﹣
 )=
)=  .
.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:
 ,(t为参数)曲线C2:
,(t为参数)曲线C2:  +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换y′=yx,后得到曲线C′.求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t= ,Q为C′上的动点,求PQ中点M到直线C3:
,Q为C′上的动点,求PQ中点M到直线C3:  (t为参数)的距离的最小值.
(t为参数)的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图所示的频率分布直方图,样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有 ( )

A. 5个 B. 6个
C. 8个 D. 10个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程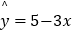 ,变量x增加一个单位时,y平均增加3个单位;
,变量x增加一个单位时,y平均增加3个单位;
③线性回归方程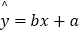 必经过点
必经过点 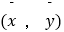 ;
;
④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校100名学生的数学测试成绩的频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20,则a的估计值是( )
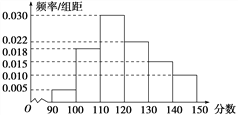
A. 130 B. 140 C. 133 D. 137
相关试题

