【题目】某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
参考答案:
【答案】(1)![]() (2)这列火车每天来回12次,才能使运营人数最多。每天最多运营人数为7920.
(2)这列火车每天来回12次,才能使运营人数最多。每天最多运营人数为7920.
【解析】试题分析:(1)先设出一次函数的解析式,再代入![]() ,利用待定系数法进行求解;(2)先设出有关未知量,结合(1)结论,得到每天运营总人数关于车厢节数
,利用待定系数法进行求解;(2)先设出有关未知量,结合(1)结论,得到每天运营总人数关于车厢节数![]() 的函数,再利用二次函数求其最值.
的函数,再利用二次函数求其最值.
试题解析:(1)设每天往返y次,每次挂x节车厢,由题意y=kx+b,当x=4时,y=16,当x=7时,y=10,
得到16=4k+b,10=7k+b.解得:k=-2,b=24,∴y=-2x+24 (4分)
设每天往返y次,每次挂x节车厢,由题意知,每天挂车厢最多时,运营人数最多,设每天运营S节车
厢,则S=xy=x(-2x+24)=-2x2+24x=-2(x-6)2+72,
所以当x=6时,Smax=72,此时y=12,则每日最多运营人数为110×72="7" 920(人).
答:这列火车每天往返12次,才能使运营人数最多,每天最多运营人数为7 920人.(10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口
 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口
要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口 北偏西
北偏西 且与该港口相距20海里的
且与该港口相距20海里的 处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以
处,并以30海里/时的航行速度沿正东方向匀速行驶,假设该小船沿直线方向以 海里/时的航行速度匀速行驶,经过
海里/时的航行速度匀速行驶,经过 小时与轮船相遇.
小时与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点
 的动直线
的动直线 与抛物线
与抛物线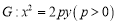 相交于
相交于 、
、 两点.当直线
两点.当直线 的斜率是
的斜率是 时,
时, .
.(1)求抛物线
 的方程;
的方程;(2)设线段
 的中垂线在
的中垂线在 轴上的截距为
轴上的截距为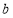 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直角梯形
 所在的平面垂直于平面
所在的平面垂直于平面 ,
,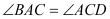
 .
.
(1)在直线
 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论.
?请证明你的结论.(2)求平面
 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在单调递增数列
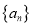 中,
中, 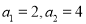 ,且
,且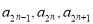 成等差数列,
成等差数列, 成等比数列,
成等比数列,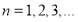 .
. (1)①求证:数列
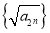 为等差数列;
为等差数列;②求数列
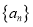 通项公式;
通项公式;(2)设数列
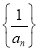 的前
的前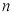 项和为
项和为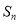 ,证明:
,证明: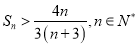 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中, 以坐标原点
 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系, 已知点
轴的非负半轴为极轴建立极坐标系, 已知点 的极坐标为
的极坐标为 ,曲线
,曲线 的参数方程为
的参数方程为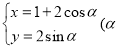 为参数).
为参数).(1)直线
 过
过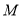 且与曲线
且与曲线 相切, 求直线
相切, 求直线 的极坐标方程;
的极坐标方程;(2)点
 与点
与点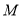 关于
关于 轴对称, 求曲线
轴对称, 求曲线 上的点到点
上的点到点 的距离的取值范围.
的距离的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试。如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚
 秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)(1)求甲距燃放点C的距离;(2)求这种烟花的垂直“冲天”高度HC

相关试题

