【题目】已知直角梯形![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() .沿
.沿![]() 将
将![]() 折起,使
折起,使![]() 至
至![]() 处,且
处,且![]() ;然后再将
;然后再将![]() 沿
沿![]() 折起,使
折起,使![]() 至
至![]() 处,且面
处,且面![]() 面
面![]() ,
,![]() 和
和![]() 在面
在面![]() 的同侧.
的同侧.

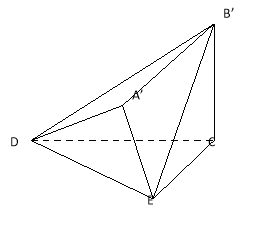
(Ⅰ) 求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求平面![]() 与平面
与平面![]() 所构成的锐二面角的余弦值.
所构成的锐二面角的余弦值.
参考答案:
【答案】(Ⅰ) 详见解析;(Ⅱ ) 平面![]() 与平面
与平面![]() 所构成的锐二面角的余弦值为
所构成的锐二面角的余弦值为![]() .
.
【解析】
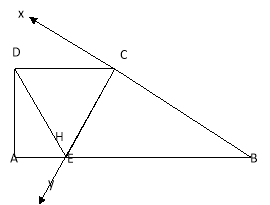
试题分析:(Ⅰ) 在直角梯形ABCD中,由平面几何知识![]() ,又
,又![]() ,可证得
,可证得![]() 平面
平面![]() ;(Ⅱ ) 建立空间直角坐标系,利用法向量可求出二面角的余弦值.
;(Ⅱ ) 建立空间直角坐标系,利用法向量可求出二面角的余弦值.
试题解析:(Ⅰ)证明:在直角梯形ABCD中,可算得![]()
根据勾股定理可得![]() ,即:
,即:![]() ,又
,又![]() ,
,![]() 平面
平面![]() ;
;
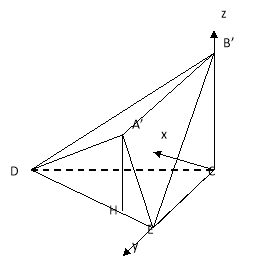
(Ⅱ) 以C为原点,CE为y轴,CB为z轴建立空间直角坐标系,如图,则![]() ,
,![]() ,
,![]() ,
,![]() ,作
,作![]() ,因为面
,因为面![]() 面
面![]() ,易知,
,易知,![]() ,且
,且![]() ,
,
从平面图形中可知:![]() ,易知面CDE的法向量为
,易知面CDE的法向量为![]()
设面PAD的法向量为![]() ,且
,且![]() .
.
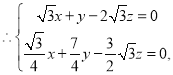 解得
解得
故所求平面![]() 与平面
与平面![]() 所构成的锐二面角的余弦值为
所构成的锐二面角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
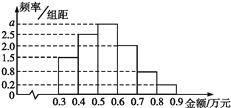
(1)直方图中的a=_____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学名著《续古摘奇算法》(杨辉著)一书中有关于三阶幻方的问题:将1, 2, 3, 4, 5, 6, 7, 8, 9分别填入
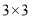 的方格中,使得每一行,每一列及对角线上的三个数的和都相等 (如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是__________.
的方格中,使得每一行,每一列及对角线上的三个数的和都相等 (如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是__________.8
3
4
1
5
9
6
7
2
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2016年1月1日起全国统一实施全面两孩政策. 为了解适龄民众对放开
生二胎政策的态度,某市选取70后作为调查对象,随机调查了10人,其中打算生二胎
的有4人,不打算生二胎的有6人.
(1)从这10人中随机抽取3人,记打算生二胎的人数为
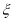 ,求随机变量
,求随机变量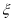 的分布列和数学期望;
的分布列和数学期望;(2)若以这10人的样本数据估计该市的总体数据,且以频率作为概率,从该市70后中随机抽取3人,记打算生二胎的人数为
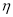 ,求随机变量
,求随机变量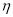 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
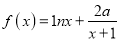 .
.(1)求
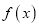 的单调区间;
的单调区间;(2)若
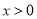 且
且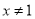 时,
时, 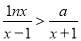 恒成立,求
恒成立,求 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】“世界睡眠日”定在每年的3月21日,某网站于2017年3月14日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2 000人参加调查,现将数据整理分组后如下表所示.
序号(i)
分组睡眠时间
组中值(mi)
频数(人数)
频率(fi)
1
[4,5)
4.5
80
2
[5,6)
5.5
520
0.26
3
[6,7)
6.5
600
0.30
4
[7,8)
7.5
5
[8,9)
8.5
200
0.10
6
[9,10]
9.5
40
0.02
(1)求出表中空白处的数据,并将表格补充完整.
(2)画出频率分布直方图.
(3)为了对数据进行分析,采用了计算机辅助计算.程序框图如图所示,求输出的S值,并说明S的统计意义.
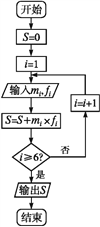
-
科目: 来源: 题型:
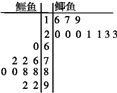
查看答案和解析>>【题目】已知某池塘养殖着鲤鱼和鲫鱼,为了估计这两种鱼的数量,养殖者从池塘中捕出这两种鱼各1 000条,给每条鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机地捕出1 000条鱼,记录下其中有记号的鱼的数目,立即放回池塘中.这样的记录做了10次,并将记录获取的数据制作成如图所示的茎叶图.
(1)根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数,并估计池塘中的鲤鱼和鲫鱼的数量;
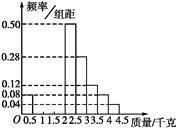
(2)为了估计池塘中鱼的总质量,现按照(1)中的比例对100条鱼进行称重,根据称重鱼的质量介于[0,4.5](单位:千克)之间,将测量结果按如下方式分成九组:第一组[0,0.5),第二组[0.5,1),…,第九组[4,4.5].如图是按上述分组方法得到的频率分布直方图的一部分.
①估计池塘中鱼的质量在3千克以上(含3千克)的条数;
②若第三组鱼的条数比第二组多7条、第四组鱼的条数比第三组多7条,请将频率分布直方图补充完整;
③在②的条件下估计池塘中鱼的质量的众数及池塘中鱼的总质量.
相关试题

