【题目】如图,某观测站在港口A的南偏西40°方向的C处,测得一船在距观测站31海里的B处,正沿着从港口出发的一条南偏东20°的航线上向港口A开去,当船走了20海里到达D处,此时观测站又测得CD等于21海里,问此时船离港口A处还有多远? 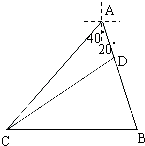
参考答案:
【答案】解:由题∠CAB=60°,设∠ACD=α,∠CDB=β,
在△CDB中,由余弦定理得 ![]() .
.
∴ ![]() ,
,
∴ ![]()
在△ACD中,
由正弦定理得 ![]() ,
,
∴ ![]() ,
,
即船离港口A处还有15海里.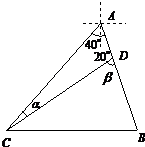
【解析】在△BDC中,先由余弦定理可得,可求cos∠CDB,进而可求sin∠CDB,由三角形的内角和定理可得sinα,再在△ACD中,由正弦定理求出AD的长;
【考点精析】通过灵活运用正弦定理的定义,掌握正弦定理:![]() 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间共有
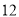 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间
 名工人中有几名优秀工人;
名工人中有几名优秀工人;(Ⅲ) 从该车间
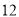 名工人中,任取2人,求恰有1名优秀工人的概率.
名工人中,任取2人,求恰有1名优秀工人的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角 所对应的边分别为
所对应的边分别为 ,
, .若
.若 ,则
,则 ( )
( )A.
 B.3 C.
B.3 C. 或3 D.3或
或3 D.3或
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
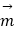 =(1,
=(1, 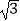 ),
), 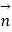 =(sinx,cosx),设函数f(x)=
=(sinx,cosx),设函数f(x)= 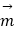
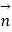
(1)求函数f(x)的最小正周期和最大值;
(2)设锐角△ABC的三个内角A,B,C的对边分别为a,b,c,若c= ,cosB=
,cosB=  ,且f(C)=
,且f(C)= 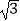 ,求b.
,求b. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
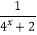 .
.
(1)求证:f(x)+f(1﹣x)= ;
;
(2)设数列{an}满足an=f(0)+f( )+f(
)+f(  )+…+f(
)+…+f( 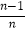 )+f(1),求an;
)+f(1),求an;
(3)设数列{an}的前项n和为Sn , 若Sn≥λan(n∈N*)恒成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甘肃省瓜州县自古就以盛产“美瓜”而名扬中外,生产的“瓜州蜜瓜”有4个系列30多个品种,质脆汁多,香甜可口,清爽宜人,含糖量达14%-19%,是消暑止渴的佳品,有诗赞曰:冰泉浸绿玉,霸刀破黄金;凉冷消晚署,清甘洗渴心,调查表明,蜜瓜的甜度与海拔高度、日照时长、温差有极强的相关性,分别用
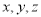 表示蜜瓜甜度与海拔高度、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标
表示蜜瓜甜度与海拔高度、日照时长、温差的相关程度,并对它们进行量化:0表示一般,1表示良,2表示优,再用综合指标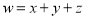 的值评定蜜瓜的等级,若
的值评定蜜瓜的等级,若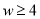 ,则为一级;若
,则为一级;若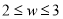 ,则为二级;若
,则为二级;若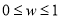 ,则为三级.近年来,周边各省也开始发展蜜瓜种植,为了了解目前蜜瓜在周边各省的种植情况,研究人员从不同省份随机抽取了10块蜜瓜种植地,得到如下结果:
,则为三级.近年来,周边各省也开始发展蜜瓜种植,为了了解目前蜜瓜在周边各省的种植情况,研究人员从不同省份随机抽取了10块蜜瓜种植地,得到如下结果:
(1)若有蜜瓜种植地110块,试估计等级为一级的蜜瓜种植地的数量;
(2)在所取样本的二级和三级蜜瓜种植地中任取2块,
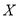 表示取到三级蜜瓜种植地的数量,求随机变量
表示取到三级蜜瓜种植地的数量,求随机变量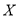 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】一河南旅游团到安徽旅游.看到安徽有很多特色食品,其中水果类较有名气的有:怀远石榴、砀山梨、徽州青枣等19种,点心类较有名气的有:一品玉带糕、徽墨酥、八公山大救驾等38种,小吃类较有名气的有:符离集烧鸡、无为熏鸭、合肥龙虾等57种.该旅游团的游客决定按分层抽样的方法从这些特产中买6种带给亲朋品尝.
(Ⅰ)求应从水果类、点心类、小吃类中分别买回的种数;
(Ⅱ)若某游客从买回的6种特产中随机抽取2种送给自己的父母,
①列出所有可能的抽取结果;
②求抽取的2种特产均为小吃的概率.
相关试题

