【题目】比较下列各组中两个值的大小 :
(1)ln0.3,ln2; (2)loga3.1,loga5.2(a>0,且a≠1);
(3)log30.2,log40.2; (4)log3π,logπ3.
参考答案:
【答案】(1)ln0.3<ln2;(2)见解析;(3)log30.2<log40.2;(4)log3π>logπ3.
【解析】试题分析:(1)构造对数函数y=lnx,利用函数的单调性判断;(2)需对底数a分类讨化;(3)由于两个对数的底数不同,故不能直接比较大小,可对这两个对数分别取倒数,再根据同底对数函数的单调性比较大小;(4)构造对数函数,并借助中间量判断.
试题解析:
(1)因为函数y=lnx是增函数,且0.3<2,
所以ln0.3<ln2.
(2)当a>1时,函数y=logax在(0,+∞)上是增函数,
又3.1<5.2,所以loga3.1<loga5.2;
当0<a<1时,函数y=logax在(0,+∞)上是减函数,
又3.1<5.2,所以loga3.1>loga5.2.
(3)因为0>log0.23>log0.24,所以![]() <
<![]() ,即log30.2<log40.2.
,即log30.2<log40.2.
(4)因为函数y=log3x是增函数,且π>3,所以log3π>log33=1,
同理,1=logππ>logπ3,即log3π>logπ3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
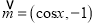 ,
,  ,设函数
,设函数 .
.(1)求函数
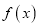 的最小正周期;
的最小正周期;(2)已知
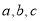 分别为三角形
分别为三角形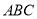 的内角对应的三边长,
的内角对应的三边长, 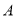 为锐角,
为锐角, 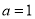 ,
,  ,且
,且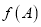 恰是函数
恰是函数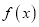 在
在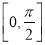 上的最大值,求
上的最大值,求 和三角形
和三角形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是实数,函数f(x)=
 (x-a).
(x-a).(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
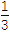 x3+
x3+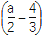 x2+
x2+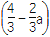 x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=elnx,g(x)=
 f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)(1)求函数g(x)的极大值;
(2)求证:1+
 +
+ +…+
+…+ >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)y=
 的单调递减区间是_____________.
的单调递减区间是_____________.(2)y=
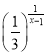 的递增区间是____________________
的递增区间是____________________
相关试题

