【题目】已知函数f(x)=elnx,g(x)=![]() f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)
(1)求函数g(x)的极大值;
(2)求证:1+![]() +
+![]() +…+
+…+![]() >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*).
参考答案:
【答案】见解析
【解析】(1)解 ∵g(x)=![]() f(x)-(x+1)=lnx-(x+1),
f(x)-(x+1)=lnx-(x+1),
∴g′(x)=![]() -1(x>0).
-1(x>0).
令g′(x)>0,解得0<x<1;
令g′(x)<0,解得x>1.
∴函数g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴g(x)极大值=g(1)=-2.
(2)证明 由(1)知x=1是函数g(x)的极大值点,也是最大值点,
∴g(x)≤g(1)=-2,即lnx-(x+1)≤-2lnx≤x-1(当且仅当x=1时等号成立),
令t=x-1,得t≥ln(t+1),t>-1,
取t=![]() (n∈N*)时,
(n∈N*)时,
则![]() >ln
>ln![]() =ln
=ln![]() ,
,
∴1>ln2,![]() >ln
>ln![]() ,
,![]() >ln
>ln![]() ,…,
,…,![]() >ln
>ln![]() ,
,
叠加得1+![]() +
+![]() +…+
+…+![]() >ln(2·
>ln(2·![]() ·
·![]() ·…·
·…·![]() )=ln(n+1).
)=ln(n+1).
即1+![]() +
+![]() +…+
+…+![]() >ln(n+1).
>ln(n+1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是实数,函数f(x)=
 (x-a).
(x-a).(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较下列各组中两个值的大小 :
(1)ln0.3,ln2; (2)loga3.1,loga5.2(a>0,且a≠1);
(3)log30.2,log40.2; (4)log3π,logπ3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
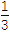 x3+
x3+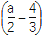 x2+
x2+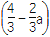 x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)y=
 的单调递减区间是_____________.
的单调递减区间是_____________.(2)y=
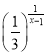 的递增区间是____________________
的递增区间是____________________ -
科目: 来源: 题型:
查看答案和解析>>【题目】设P、Q为两个非空集合,定义集合P+Q={m+n| m∈P,n∈Q},若P={0,2,5}, Q={1,2,6},则P+Q中元素的个数为 ( )
A. 9 B. 8 C. 7 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
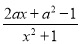 ,其中a∈R.
,其中a∈R. (I)当a=1时,求曲线y=f(x)在原点处的切线方程;
(II)求f(x)的极值.
相关试题

