【题目】半径小于![]() 的圆
的圆![]() 经过点
经过点![]() ,圆心在直线
,圆心在直线![]() 上,并且与直线
上,并且与直线![]() 相交所得的弦长为
相交所得的弦长为![]() .
.
(![]() )求圆
)求圆![]() 的方程.
的方程.
(![]() )已知点
)已知点![]() ,动点
,动点![]() 到圆
到圆![]() 的切线长等于到
的切线长等于到![]() 的距离,求
的距离,求![]() 的轨迹方程.
的轨迹方程.
参考答案:
【答案】(![]() )
)![]() (
(![]() )
)![]()
【解析】试题分析:
(1)根据圆心在直线![]() 上可设其坐标为
上可设其坐标为![]() ,故半径为
,故半径为![]() =
=
![]() ,然后根据弦长公式可得关于
,然后根据弦长公式可得关于![]() 的方程,求得
的方程,求得![]() 经验证可得圆的方程。
经验证可得圆的方程。
(2)设![]() 点坐标为
点坐标为![]() ,切点为
,切点为![]() ,则
,则![]() ,由两点间的距离公式和切线长公式可得轨迹方程。
,由两点间的距离公式和切线长公式可得轨迹方程。
试题解析:
(![]() )由圆心在直线
)由圆心在直线![]() 上可设圆心
上可设圆心![]() ,
,
则圆半径![]() ,
,
∴ 圆![]() 方程为
方程为![]() ,
,
故圆心![]() 到直线
到直线![]() 的距离
的距离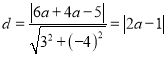 ,
,
又圆与直线所交得弦长![]() ,
,
∴ ![]() ,
,
即,
整理得![]()
解得![]() 或
或![]() ,
,
当![]() 时,
时, ![]() ,符合要求.
,符合要求.
当![]() 时,
时, ![]() ,不合题意,舍去。
,不合题意,舍去。
∴ 圆![]() 的方程为
的方程为![]() .
.
(![]() )设
)设![]() 点坐标为
点坐标为![]() ,切点为
,切点为![]() .
.
则有| ![]() ,|
,| ![]() ,
,
∵ 动点![]() 到圆
到圆![]() 的切线长等于到点
的切线长等于到点![]() 距离,
距离,
∴![]() ,
,
又切线长| ![]()
∴ ![]() ,
,
∴ ![]() ,
,
整理得![]() ,
,
即点![]() 轨迹为直线
轨迹为直线![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为 ,点
,点 在抛物线
在抛物线 上,且
上,且 。
。(Ⅰ)求抛物线
 的标准方程及实数
的标准方程及实数 的值;
的值;(Ⅱ)直线
 过抛物线
过抛物线 的焦点
的焦点 ,且与抛物线
,且与抛物线 交于
交于 两点,若
两点,若 (
( 为坐标原点)的面积为
为坐标原点)的面积为 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,其中
,其中 为常数.
为常数.(1)证明:
 ;
;(2)是否存在
 ,使得
,使得 为等差数列?并说明理由.
为等差数列?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
 的左焦点为
的左焦点为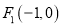 ,且过点
,且过点 .
. 
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线
 与椭圆E交于
与椭圆E交于 两点,与
两点,与 的交点为
的交点为 ,且满足.
,且满足. 

①若
 ,求:
,求: 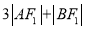 的值;
的值;②设点
 是椭圆E的左顶点,点
是椭圆E的左顶点,点 关于
关于 轴的对称点为点
轴的对称点为点 ,试探究:在线段
,试探究:在线段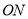 上是否存在一个定点
上是否存在一个定点 ,使得直线
,使得直线 过定点
过定点 ,如果存在,求出点
,如果存在,求出点 的坐标;如果不存在,请说明理由。
的坐标;如果不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是定义在
是定义在 上的偶函数,
上的偶函数, 的图象与
的图象与 的图象关于直线
的图象关于直线 对称,且当
对称,且当 时,
时, .
.(
 )求
)求 的解析式.
的解析式.(
 )若
)若 在
在 上为增函数,求
上为增函数,求 的取值范围.
的取值范围.(
 )是否存在正整数
)是否存在正整数 ,使
,使 的图象的最高点落在直线
的图象的最高点落在直线 上?若存在,求出
上?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线l:ax+
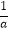 y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D.给出下列命题:p:a>0,S△AOB=
y﹣1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D.给出下列命题:p:a>0,S△AOB=  ,q:a>0,|AB|<|CD|.则下面命题正确的是( )
,q:a>0,|AB|<|CD|.则下面命题正确的是( )
A.p∧q
B.¬p∧¬q
C.p∧¬q
D.¬p∧q -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知多面体
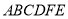 中,四边形
中,四边形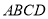 为矩形,
为矩形, 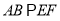 ,
, 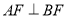 ,平面
,平面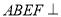 平面
平面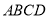 ,
, 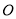 、
、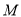 分别为
分别为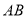 、
、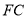 的中点.
的中点.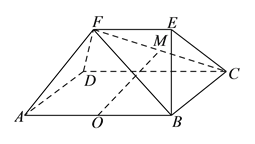
(
 )求证:
)求证: 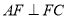 .
.(
 )求证:
)求证: 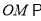 平面
平面 .
.(
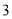 )若过
)若过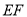 的平面交
的平面交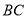 于点
于点 ,交
,交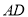 于
于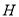 ,求证:
,求证: 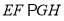 .
.
相关试题

