【题目】已知函数f(x)= 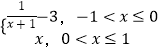 ,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为 .
,若函数g(x)=f(x)﹣mx﹣m在(﹣1,1]内有且仅有两个不同的零点,则实数m的取值范围为 .
参考答案:
【答案】( ![]() ,﹣2]∪(0,
,﹣2]∪(0,![]() ]
]
【解析】解:由g(x)=f(x)﹣mx﹣m=0,即f(x)=m(x+1),
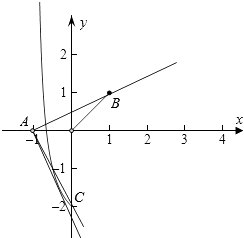
分别作出函数f(x)和y=h(x)=m(x+1)的图象如图:
由图象可知f(1)=1,h(x)表示过定点A(﹣1,0)的直线,
当h(x)过(1,1)时,m= ![]() ,此时两个函数有两个交点,
,此时两个函数有两个交点,
此时满足条件的m的取值范围是0<m≤ ![]() ,
,
当h(x)过(0,﹣2)时,h(0)=﹣2,解得m=﹣2,此时两个函数有两个交点,
当h(x)与f(x)相切时,两个函数只有一个交点,此时 ![]() x﹣3=m(x+1)即m(x+1)2+3(x+1)﹣1=0,
x﹣3=m(x+1)即m(x+1)2+3(x+1)﹣1=0,
当m=0时,只有1解,当m≠0,由△=9+4m=0得m=﹣ ![]() ,此时直线和f(x)相切,
,此时直线和f(x)相切,
∴要使函数有两个零点,则﹣ ![]() <m≤﹣2或0<m≤
<m≤﹣2或0<m≤ ![]() .
.
所以答案是:( ![]() ,﹣2]∪(0,
,﹣2]∪(0, ![]() ].
].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中,  分别为
分别为 的中点,点
的中点,点 为线段
为线段 上的一点,将
上的一点,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.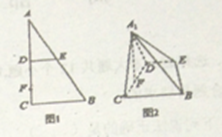
(1)求证:
 ;
;(2)线段
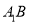 上是否存在点
上是否存在点 ,使
,使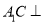 平面
平面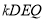 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数
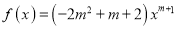 为偶函数.
为偶函数.(1)求
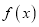 的解析式;
的解析式;(2)若函数
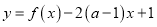 在区间
在区间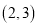 上为单调函数,求实数
上为单调函数,求实数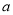 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,平面
中,平面 平面
平面 ,
, ,
, 是等边三角形,已知
是等边三角形,已知 ,
, .
.
(1)设
 是
是 上的一点,证明:平面
上的一点,证明:平面 平面
平面 ;
;(2)求四棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定义域;
(2)若不等式f(x)≤c的恒成立,求实数c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)(sinx+cosx)2+2cos2x﹣2
(1)求函数f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值时x取值集合;
(3)当x∈[ ,
, 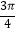 ]时,求函数f(x)的值域.
]时,求函数f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在南北方向有一条公路,一半径为100m的圆形广场(圆心为O)与此公路一边所在直线l相切于点A.点P为北半圆弧(弧APB)上的一点,过P作直线l的垂线,垂足为Q.计划在△PAQ内(图中阴影部分)进行绿化.设△PAQ的面积为S(单位:m2).

(1)设∠BOP=α(rad),将S表示为α的函数;
(2)确定点P的位置,使绿化面积最大,并求出最大面积.
相关试题

