【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).

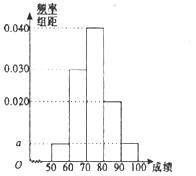
(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式: 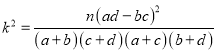 ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() 分;(Ⅲ)见解析.
分;(Ⅲ)见解析.
【解析】试题分析:(1)根据频率分布直方图矩形面积和为1可求出![]() ;
;
(2)根据每个小矩形的中点乘以面积求和即可;
(3)套用![]() 的计算公式求值,查表下结论即可.
的计算公式求值,查表下结论即可.
试题解析:
(Ⅰ)由频率分布直方图各小长方形面积总和为1,可知
![]() ,故
,故![]() .
.
(Ⅱ) 由频率分布直方图知各小组依次是![]() ,
,
其中点分别为![]() 对应的频率分别为
对应的频率分别为![]() ,
,
故可估计平均分
![]() (分)
(分)
(Ⅲ)由频率分布直方图知,晋级成功的频率为![]() ,
,
故晋级成功的人数为![]() (人),故填表如下
(人),故填表如下
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | 34 | 50 |
女 | 9 | 41 | 50 |
合计 | 25 | 75 | 100 |
假设“晋级成功”与性别无关,
根据上表数据代入公式可得![]() ,
,
所以有超过85%的把握认为“晋级成功”与性别有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形
 中,
中,  ,
,  为
为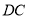 的中点,将
的中点,将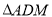 沿
沿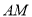 折起,使得平面
折起,使得平面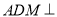 平面
平面 ,设点
,设点 是线段
是线段 上的一动点(不与
上的一动点(不与 ,
, 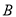 重合).
重合).
(Ⅰ)当
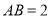 时,求三棱锥
时,求三棱锥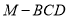 的体积;
的体积;(Ⅱ)求证:
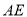 不可能与
不可能与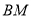 垂直.
垂直. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B(其中
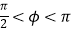 ),那么这一天6时至14时温差的最大值是°C;与图中曲线对应的函数解析式是 .
),那么这一天6时至14时温差的最大值是°C;与图中曲线对应的函数解析式是 . 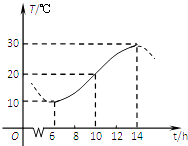
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
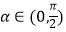 ,向量
,向量 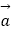 =(cosα,sinα),
=(cosα,sinα), 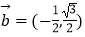 .
.
(1)证明:向量 与
与 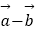 垂直;
垂直;
(2)当|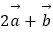 |=|
|=| 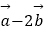 |时,求角α.
|时,求角α. -
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥的三组相对棱(相对的棱是指三棱锥中成异面直线的一组棱)分别相等,且长分别为
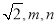 ,其中
,其中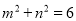 ,则该三棱锥体积的最大值为
,则该三棱锥体积的最大值为A.
 B.
B. 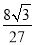 C.
C. 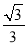 D.
D. 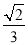
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心在直线上
 ,且与直线
,且与直线 相切于点
相切于点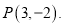
(1)求圆C的方程;
(2)是否存在过点
 的直线
的直线 与圆C交于
与圆C交于 两点,且
两点,且 的面积为
的面积为 (O为坐标原点),若存在,求出直线
(O为坐标原点),若存在,求出直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱
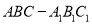 中,
中, 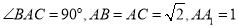 ,点
,点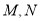 分别为
分别为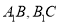 的中点.
的中点.(1)求证:
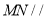 平面
平面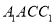 ;
;(2)求三棱锥
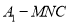 的体积(锥体的体积公式
的体积(锥体的体积公式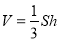 ,其中
,其中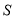 为底面面积,
为底面面积,  为高)
为高)
相关试题

