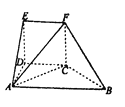
【题目】如图,几何体![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 是正方形,
是正方形, ![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 的腰长为
的腰长为![]() 的等腰直角三角形.
的等腰直角三角形.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
参考答案:
【答案】(I)证明过程见解析;(Ⅱ)二面角![]() 的大小为
的大小为![]() .
.
【解析】试题分析:(Ⅰ)证明![]() ,然后证明
,然后证明![]() 平面
平面![]() ,推出
,推出![]() 平面
平面![]() ,利用直线与平面垂直的性质定理证明
,利用直线与平面垂直的性质定理证明![]() ;(Ⅱ)建立空间立体直角坐标系
;(Ⅱ)建立空间立体直角坐标系![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的法向量,求出法向量之间的夹角即可求出二面角
的法向量,求出法向量之间的夹角即可求出二面角![]() 的大小.
的大小.
试题解析:
(I)证明:因为![]() 是腰长为
是腰长为![]() 的等腰直角三角形,所以
的等腰直角三角形,所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
(Ⅱ)解:以点![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴建立如下图
轴建立如下图
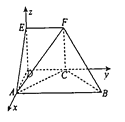
所示的空间直角坐标系:
因为![]() 是腰长为
是腰长为![]() 的等腰直角三角形,
的等腰直角三角形,
所以![]() ,
, ![]() .
.
所以![]() ,
,
![]() .
.
所以![]() .
.
则点![]() .
.
则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由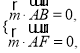 得
得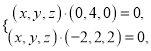 得
得![]() 得
得![]()
令![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量;
的一个法向量;
易知平面![]() 的一个法向量
的一个法向量![]() ;
;
设二面角![]() 的大小为
的大小为![]() ,则
,则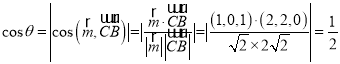 ,
,
又![]() ,解得
,解得![]() .
.
故二面角![]() 的大小为
的大小为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是( )
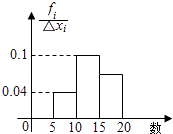
A.12.5 12.5
B.12.5 13
C.13 12.5
D.13 13 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3﹣ax2﹣3x.
(1)若a=4时,求f(x)在x∈[1,4]上的最大值和最小值;
(2)若f(x)在x∈[2,+∞]上是增函数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】按如图所示的程序框图操作: (Ⅰ)写出输出的数所组成的数集.若将输出的数按照输出的顺序从前往后依次排列,则得到数列{an},请写出数列{an}的通项公式;
(Ⅱ)如何变更A框内的赋值语句,使得根据这个程序框图所输出的数恰好是数列{2n}的前7项?
(Ⅲ)如何变更B框内的赋值语句,使得根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个)
2
3
4
5
加工的时间y(小时)
2.5
3
4
4.5
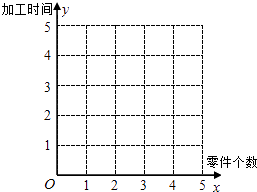
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程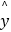 =
= 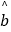 x+
x+ 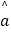 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线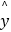 =bx+a,其中b=
=bx+a,其中b= 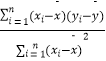 =
= 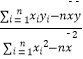 ,a=
,a=  ﹣b
﹣b  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图甲所示,据此解答如下问题:
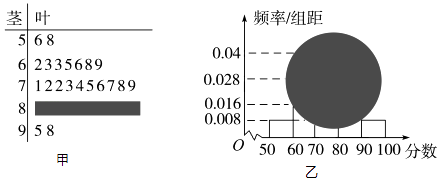
(1)求该班全体男生的人数;
(2)求分数在[80,90)之间的男生人数,并计算频率公布直方图如图乙中[80,90)之间的矩形的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为
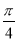 ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.

(Ⅰ)试问:购买该商品的顾客在哪家商场中奖的可能性大?说明理由;
(Ⅱ)记在乙商场购买该商品的顾客摸到篮球的个数为
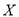 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
相关试题

