【题目】已知函数f(x)=x3﹣ax2﹣3x.
(1)若a=4时,求f(x)在x∈[1,4]上的最大值和最小值;
(2)若f(x)在x∈[2,+∞]上是增函数,求实数a的取值范围.
参考答案:
【答案】
(1)解:a=4时,f(x)=x3﹣4x2﹣3x,
∴f′(x)=3x2﹣8x﹣3,
∴函数在[1,3]上单调递减,[3,4]上单调递增,
∴f(x)在x∈[1,4]上的最大值为f(1)=﹣6,最小值为f(3)=﹣18
(2)解:在x∈[2,+∞]上,f′(x)=3x2﹣2ax﹣3≥0,
可得a≤ ![]() 在x∈[2,+∞]上恒成立,
在x∈[2,+∞]上恒成立,
∴只要求 ![]() 的最小值即可,而y=
的最小值即可,而y= ![]() .
.
y′= ![]() 恒大于零,
恒大于零,
∴y在R上为增函数,∴ymin= ![]() ,
,
∴a≤ ![]()
【解析】(1)求导数,确定函数在[1,3]上单调递减,[3,4]上单调递增,即可求f(x)在x∈[1,4]上的最大值和最小值;(2)在x∈[2,+∞]上,f′(x)=3x2﹣2ax﹣3≥0可得a≤ ![]() 在x∈[2,+∞]上恒成立,只要求
在x∈[2,+∞]上恒成立,只要求 ![]() 的最小值即可得到a的取值范围.
的最小值即可得到a的取值范围.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是定义在R上的奇函数,当x>0时,f′(x)sinx+f(x)cosx>0且f(
 )=1,则f(x)sinx≤1的整数解的集合为 .
)=1,则f(x)sinx≤1的整数解的集合为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】f(x)=lnx﹣ax+1.
(1)求f(x)的单调增区间.
(2)求出f(x)的极值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别是( )
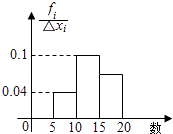
A.12.5 12.5
B.12.5 13
C.13 12.5
D.13 13 -
科目: 来源: 题型:
查看答案和解析>>【题目】按如图所示的程序框图操作: (Ⅰ)写出输出的数所组成的数集.若将输出的数按照输出的顺序从前往后依次排列,则得到数列{an},请写出数列{an}的通项公式;
(Ⅱ)如何变更A框内的赋值语句,使得根据这个程序框图所输出的数恰好是数列{2n}的前7项?
(Ⅲ)如何变更B框内的赋值语句,使得根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,几何体
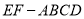 中,
中,  平面
平面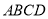 ,
, 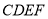 是正方形,
是正方形, 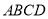 为直角梯形,
为直角梯形, 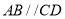 ,
, 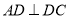 ,
, 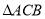 的腰长为
的腰长为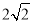 的等腰直角三角形.
的等腰直角三角形.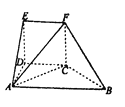
(Ⅰ)求证:
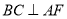 ;
;(Ⅱ)求二面角
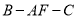 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个)
2
3
4
5
加工的时间y(小时)
2.5
3
4
4.5
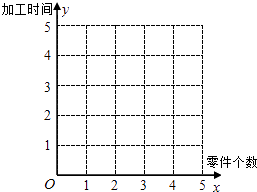
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程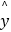 =
= 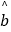 x+
x+ 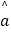 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间? 参考公式:回归直线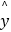 =bx+a,其中b=
=bx+a,其中b= 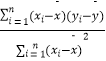 =
= 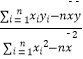 ,a=
,a= 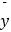 ﹣b
﹣b  .
.
相关试题

