【题目】已知函数![]() 在
在![]() 处有极值10.
处有极值10.
(Ⅰ)求实数![]() ,
, ![]() 的值;
的值;
(Ⅱ)设![]() 时,讨论函数
时,讨论函数![]() 在区间
在区间![]() 上的单调性.
上的单调性.
参考答案:
【答案】(Ⅰ)![]() ,
, ![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】试题分析:(Ⅰ) ![]() ,
, ![]() 在
在![]() 处有极值10,所以
处有极值10,所以![]() 且
且![]() ;
;
(Ⅱ)求导得函数在R上的单调性,再讨论函数定义域在哪个区间即可.
试题解析:
(Ⅰ)![]() 定义域为
定义域为![]() ,
, ![]() ,
,
∵![]() 在
在![]() 处有极值10.
处有极值10.
∴![]() 且
且![]() .
.
即![]()
解得:  或
或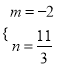
当![]() ,
, ![]() 时,
时, ![]() ,
,
当![]() ,
, ![]() 时,
时, ![]() ,
,
∴![]() 在处
在处![]() 处有极值10时,
处有极值10时, ![]() ,
, ![]() .
.
(Ⅱ)由(Ⅰ)可知![]() ,其单调性和极值分布情况如表:
,其单调性和极值分布情况如表:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| 增 | 极大 | 减 | 极小 | 增 |
①当![]() 且
且![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上单调递减;
上单调递减;
②当![]()
![]() ,即
,即![]() 时,
时, ![]() 在区间
在区间![]() 上的单调递减,在区间
上的单调递减,在区间![]() 上单调递增;
上单调递增;
③当![]() 时,
时, ![]() 在区间
在区间![]() 上单调递增.
上单调递增.
综上所述,当![]() 时函数
时函数![]() 在区间
在区间![]() 上的单调性为:
上的单调性为:
![]() 时,单调递减;
时,单调递减;
![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
![]() 时,
时, ![]() 在
在![]() 上单调递增.
上单调递增.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设F1 , F为椭圆C1:
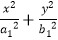 =1,(a1>b1>0)与双曲线C2的公共左、右焦点,它们在第一象限内交于点M,△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2,若椭圆C1的离心率e∈[
=1,(a1>b1>0)与双曲线C2的公共左、右焦点,它们在第一象限内交于点M,△MF1F2是以线段MF1为底边的等腰三角形,且|MF1|=2,若椭圆C1的离心率e∈[  ,
,  ],则双曲线C2的离心率的取值范围是( )
],则双曲线C2的离心率的取值范围是( )
A.[ ,
,  ]
]
B.[ ,++∞)
,++∞)
C.(1,4]
D.[ ,4]
,4] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b∈R,向量
 =(x , 1),
=(x , 1),  =(﹣1,b﹣x),函数f(x)=a﹣
=(﹣1,b﹣x),函数f(x)=a﹣ 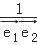 是偶函数.
是偶函数.
(1)求b的值;
(2)若在函数定义域内总存在区间[m,n](m<n),使得y=f(x)在区间[m,n]上的函数值组成的集合也是[m,n],求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 和
和 的通项公式分别为
的通项公式分别为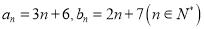 ,将集合
,将集合
 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列 ;将集合
;将集合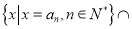
 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列 .
.(1)求数列
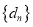 的通项公式
的通项公式 ;
;(2)求数列
 的通项公式
的通项公式 ;
;(3)设数列
 的前
的前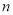 项和为
项和为 ,求数列
,求数列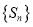 的通项公式
的通项公式 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为坐标原点,双曲线C:
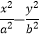 =1(a>0,b>0)的左焦点为F(﹣c,0)(c>0),以OF为直径的圆交双曲线C的渐近线于A,B,O三点,且(
=1(a>0,b>0)的左焦点为F(﹣c,0)(c>0),以OF为直径的圆交双曲线C的渐近线于A,B,O三点,且( 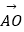 +
+ 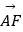 )
)  =0,若关于x的方程ax2+bx﹣c=0的两个实数根分别为x1和x2 , 则以|x1|,|x2|,2为边长的三角形的形状是( )
=0,若关于x的方程ax2+bx﹣c=0的两个实数根分别为x1和x2 , 则以|x1|,|x2|,2为边长的三角形的形状是( )
A.钝角三角形
B.直角三角形
C.锐角三角形
D.等腰直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来我国电子商务行业迎来发展的新机遇,2016年双11期间,某购物平台的销售业
绩高达1207亿人民币。与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.
(1)请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为随机变量
 :
:①求对商品和服务全好评的次数
 的分布列;
的分布列;②求
 的数学期望和方差.
的数学期望和方差.
(
 ,其中
,其中 )
)对服务好评
对服务不满意
合计
对商品好评
140
对商品不满意
10
合计
200
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
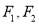 分别为椭圆
分别为椭圆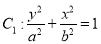 的上、下焦点,
的上、下焦点, 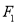 是抛物线
是抛物线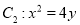 的焦点,点
的焦点,点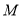 是
是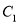 与
与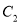 在第二象限的交点,且
在第二象限的交点,且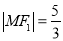 .
.(1)求椭圆
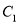 的方程;
的方程;(2)与圆
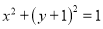 相切的直线
相切的直线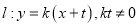 交椭圆
交椭圆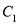 于
于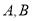 ,
,若椭圆
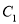 上一点
上一点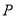 满足
满足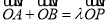 ,求实数
,求实数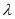 的取值范围.
的取值范围.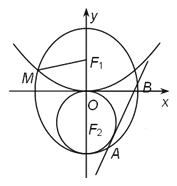
相关试题

