【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
参考答案:
【答案】(1) 甲的平均数为8,标准差为![]() ,乙的平均数为8,标准差为
,乙的平均数为8,标准差为![]() (2) 选择乙参加射箭比赛
(2) 选择乙参加射箭比赛
【解析】
试题分析:(1)根据所给的数据,利用平均数和标准差的计算公式,分别求解,即可得到答案;(2)比较甲和乙的标准差的大小,根据标准差越小,其稳定性越好,即可得到答案
试题解析:(1)根据题中所给数据,则甲的平均数为![]() ,
,
乙的平均数为![]() ,
,
甲的标准差为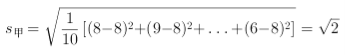 ,
,
乙的标准差为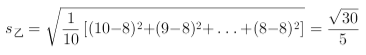 ,
,
故甲的平均数为8,标准差为![]() ,乙的平均数为8,标准差为
,乙的平均数为8,标准差为![]() ;
;
(2)![]() ,且
,且![]() ,
,
![]() 乙的成绩较为稳定, 故选择乙参加射箭比赛.
乙的成绩较为稳定, 故选择乙参加射箭比赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
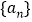 中,
中,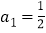 ,点
,点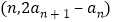 (
( )在直线y = x上,
)在直线y = x上,(Ⅰ)计算a2,a3,a4的值;
(Ⅱ)令bn=an+1﹣an﹣1,求证:数列{bn}是等比数列;
(Ⅲ)设Sn、Tn分别为数列{an}、{bn}的前n项和,是否存在实数λ,使得数列
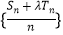 为等差数列?若存在,试求出λ的值;若不存在,请说明理由.
为等差数列?若存在,试求出λ的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】据俄罗斯新罗西斯克2015年5月17日电 记者吴敏、郑文达报道:当地时间17日,参加中俄“海上联合-2015(Ⅰ)”军事演习的9艘舰艇抵达地中海预定海域,混编组成海上联合集群.接到命令后我军在港口M要将一件重要物品用小艇送到一艘正在航行的俄军轮船上,在小艇出发时,轮船位于港口M北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值并说明你的推理过程;
(3)是否存在v,使得小艇以v海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定v的取值范围;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式:
(1)
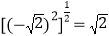 ;
;(2)已知
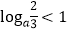 ,则
,则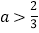 ;
;(3)函数
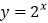 的图象与函数
的图象与函数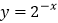 的图象关于y轴对称;
的图象关于y轴对称;(4)函数
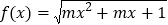 的定义域是R,则m的取值范围是
的定义域是R,则m的取值范围是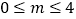 ;
;(5)函数
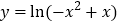 的递增区间为
的递增区间为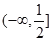 .
.正确的有______________________.(把你认为正确的序号全部写上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1+2x.
(1)求函数f(x)的解析式;
(2)画出函数f(x)的图像;
(3)写出函数f(x)的单调区间及值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
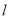 的参数方程为
的参数方程为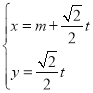 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,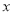 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为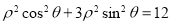 ,且曲线
,且曲线 的左焦点
的左焦点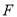 在直线
在直线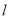 上.
上.(1)若直线
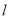 与曲线
与曲线 交于
交于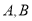 两点,求
两点,求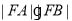 的值;
的值;(2)求曲线
 的内接矩形的周长的最大值.
的内接矩形的周长的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
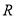 上的函数
上的函数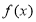 的导函数为
的导函数为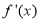 ,且满足
,且满足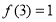 ,
,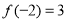 ,当
,当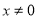 时有
时有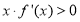 恒成立,若非负实数
恒成立,若非负实数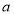 、
、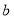 满足
满足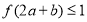 ,
,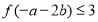 ,则
,则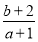 的取值范围为 .
的取值范围为 .
相关试题

