搜索
【题目】如图，在平面直角坐标系
中，以
轴为始边做两个锐角
，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为
（1）求
的值； （2）求
的值。
参考答案：
【答案】（1）
（2）
【解析】
试题（1）根据题意，由三角函数的定义可得
与
的值，进而可得出
与
的值，从而可求
与
的值就，结合两角和正切公式可得答案；（2）由两角和的正切公式，可得出
的值，再根据
的取值范围，可得出
的取值范围，进而可得出的值.
由条件得cosα＝
，cosβ＝
.
∵ α，β为锐角，
∴ sinα＝
＝
，sinβ＝
＝
.
因此tanα＝
＝7，tanβ＝
＝
.
(1) tan(α＋β)＝
＝
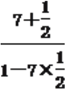＝－3.
(2) ∵ tan2β＝
＝
＝
，
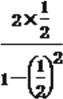∴ tan(α＋2β)＝
＝
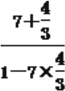＝－1.
∵ α，β为锐角，∴ 0<α＋2β<
，∴ α＋2β＝
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x﹣alnx（a∈R）
（1）当a=2时，求曲线y=f（x）在点A（1，f（1））处的切线方程；
（2）求函数f（x）的极值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
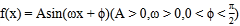的图象如图所示，则下列说法正确的是（ ）
A. 函数
的周期为
B. 函数
在
上单调递增C. 函数
的图象关于点
对称D. 把函数
的图象向右平移
个单位，所得图象对应的函数为奇函数 -
科目： 来源： 题型：
查看答案和解析>>【题目】在某次测试中，卷面满分为100分，考生得分为整数，规定60分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响，对午休和不午休的考生进行了测试成绩的统计，数据如下表：
分数段
0～39
40～49
50～59
60～69
70～79
80～89
90～100
午休考生人数
29
34
37
29
23
18
10
不午休考生人数
20
52
68
30
15
12
3
（1）根据上述表格完成下列列联表：
及格人数
不及格人数
合计
午休
不午休
合计
（2）判断“能否在犯错误的概率不超过0.010的前提下认为成绩及格与午休有关”？
0.10
0.05
0.010
0.001
2.706
3.841
6.635
10.828
（参考公式：
，其中
） -
科目： 来源： 题型：
查看答案和解析>>【题目】写出下列命题的否定,并判断其真假：
（1）任何有理数都是实数；
（2）存在一个实数
，能使
成立. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形OABC中，O为坐标原点，点A的坐标为（10，0），点C的坐标为（0，10），分别将线段OA和AB十等分，分点分别记为A1 ， A2 ， …，A9和B1 ， B2 ， …，B9 ， 连接OBi ， 过Ai作x轴的垂线与OBi ， 交于点
． 
（1）求证：点 都在同一条抛物线上，并求抛物线E的方程；
（2）过点C作直线l与抛物线E交于不同的两点M，N，若△OCM与△OCN的面积之比为4：1，求直线l的方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥DC，AA1=1，AB=3k，AD=4k，BC=5k，DC=6k，（k＞0）
（1）求证：CD⊥平面ADD1A1
（2）若直线AA1与平面AB1C所成角的正弦值为
，求k的值
（3）现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱，规定：若拼成的新四棱柱形状和大小完全相同，则视为同一种拼接方案，问共有几种不同的拼接方案？在这些拼接成的新四棱柱中，记其中最小的表面积为f（k），写出f（k）的解析式．（直接写出答案，不必说明理由）
相关试题
