【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k,(k>0)
(1)求证:CD⊥平面ADD1A1
(2)若直线AA1与平面AB1C所成角的正弦值为 ![]() ,求k的值
,求k的值
(3)现将与四棱柱ABCD﹣A1B1C1D1形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式.(直接写出答案,不必说明理由)
参考答案:
【答案】
(1)
证明:取DC的中点E,连接BE,∵AB∥ED,AB=ED=3k,
∴四边形ABED是平行四边形,
∴BE∥AD,且BE=AD=4k,∴BE2+EC2=(4k)2+(3k)2=(5k)2=BC2,∴∠BEC=90°,∴BE⊥CD,
又∵BE∥AD,∴CD⊥AD.
∵侧棱AA1⊥底面ABCD,∴AA1⊥CD,
∵AA1∩AD=A,∴CD⊥平面ADD1A1
(2)
解:以D为坐标原点, ![]() 、
、 ![]() 、
、 ![]() 的方向为x,y,z轴的正方向建立空间直角坐标系,
的方向为x,y,z轴的正方向建立空间直角坐标系,
则A(4k,0,0),C(0,6k,0),B1(4k,3k,1),A1(4k,0,1).
∴ ![]() ,
, ![]() ,
, ![]() .
.
设平面AB1C的一个法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,取y=2,则z=﹣6k,x=3.∴
,取y=2,则z=﹣6k,x=3.∴ ![]() .
.
设AA1与平面AB1C所成角为θ,则 ![]() =
=  =
= ![]() =
= ![]() ,解得k=1,故所求k=1.
,解得k=1,故所求k=1.
(3)
解:由题意可与左右平面ADD1A1,BCC1B1,上或下面ABCD,A1B1C1D1拼接得到方案新四棱柱共有此4种不同方案.
写出每一方案下的表面积,通过比较即可得出f(k)= 
【解析】(1)取DC得中点E,连接BE,可证明四边形ABED是平行四边形,再利用勾股定理的逆定理可得BE⊥CD,即CD⊥AD,又侧棱AA1⊥底面ABCD,可得AA1⊥DC,利用线面垂直的判定定理即可证明.(2)通过建立空间直角坐标系,求出平面的法向量与斜线的方向向量的夹角即可得出;(3)由题意可与左右平面ADD1A1 , BCC1B1 , 上或下面ABCD,A1B1C1D1拼接得到方案新四棱柱共有此4种不同方案.写出每一方案下的表面积,通过比较即可得出f(k).
【考点精析】利用直线与平面垂直的判定和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,以
中,以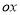 轴为始边做两个锐角
轴为始边做两个锐角 ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为

(1)求
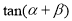 的值; (2)求
的值; (2)求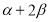 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】写出下列命题的否定,并判断其真假:
(1)任何有理数都是实数;
(2)存在一个实数
 ,能使
,能使 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1 , A2 , …,A9和B1 , B2 , …,B9 , 连接OBi , 过Ai作x轴的垂线与OBi , 交于点
 .
. 
(1)求证:点 都在同一条抛物线上,并求抛物线E的方程;
都在同一条抛物线上,并求抛物线E的方程;
(2)过点C作直线l与抛物线E交于不同的两点M,N,若△OCM与△OCN的面积之比为4:1,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品原来每件售价为25元,年销售量8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到
 元.公司拟投入
元.公司拟投入 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入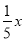 万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(wx+φ)(w>0,0<φ<π)的周期为π,图象的一个对称中心为(
 ,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个
,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个  单位长度后得到函数g(x)的图象.
单位长度后得到函数g(x)的图象.
(1)求函数f(x)与g(x)的解析式
(2)是否存在x0∈( ),使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数,若不存在,说明理由;
),使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数,若不存在,说明理由;
(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某种书籍每册的成本费
 (元)与印刷册数
(元)与印刷册数 (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.


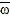




4.83
4.22
0.3775
60.17
0.60
-39.38
4.8
表中
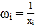 ,
,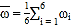 .
.为了预测印刷20千册时每册的成本费,建立了两个回归模型:
 ,
, .
.(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中选择的模型,求
 关于
关于 的回归方程,并预测印刷20千册时每册的成本费.
的回归方程,并预测印刷20千册时每册的成本费.附:对于一组数据
 ,
, ,…,
,…, ,其回归方程
,其回归方程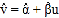 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
, .
.
相关试题

