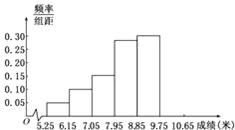
【题目】某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
(1)求这次铅球测试成绩合格的人数;
(2)若由直方图来估计这组数据的中位数,指出它在第几组内,并说明理由;
(3)若参加此次测试的学生中,有9人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知a、b的成绩均为优秀,求两人至少有1人入选的概率。
参考答案:
【答案】(1)36(2)4(3)![]()
【解析】试题分析:(1)由频率分布直方图的面积和为1,可求得第6组频率为0.14,从而求得总人数为50人,由图可知第4、5、6组成绩均合格,由频率和乘以总人数可求。(2)直方图中位数在面积为0.5的位置,前三组的频率和为0.28,前四组的频率和为0.56,所以中位数位于第4组内。(3)设成绩优秀的9人分别为a,b,c,d,e,f,g,h,k,采用枚举法,算出总情况36种,和满足条件的情况共15种,由古典概型可求得概率。
试题解析:(1)第6小组的频率为1﹣(0.04+0.10+0.14+0.28+0.30)=0.14,
∴此次测试总人数为![]() (人).
(人).
∴第4、5、6组成绩均合格,人数为(0.28+0.30+0.14)×50=36(人).
(2)直方图中中位数两侧的面积相等,即频率相等.前三组的频率和为0.28,前四组的频率和为0.56,∴中位数位于第4组内.
(3)设成绩优秀的9人分别为a,b,c,d,e,f,g,h,k,
则选出的2人所有可能的情况为:ab,ac,ad,ae,af,ag,ah,ak;bc,bd,be,bf,
bg,bh,bk;cd,ce,cf,cg,ch,ck;de,df,dg,dh,dk;ef,eg,eh,ek;fg,fh,fk;gh,gk;hk.共36种,其中a、b到少有1人入选的情况有15种,
∴a、b两人至少有1人入选的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个结论,其中正确的个数为( ). ①已
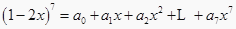 ,则
,则 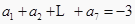
②过原点作曲线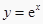 的切线,则切线方程为
的切线,则切线方程为 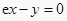 (其中e为自然对数的底数);
(其中e为自然对数的底数);
③已知随机变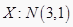
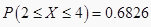 ,则
,则 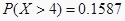
④已知n为正偶数,用数学归纳法证明等式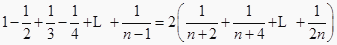 时,若假设
时,若假设  时,命题为真,则还需利用归纳假设再证明
时,命题为真,则还需利用归纳假设再证明 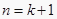 时等式成立,即可证明等式对一切正偶数n都成立.
时等式成立,即可证明等式对一切正偶数n都成立.
⑤在回归分析中,常用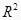 来刻画回归效果,在线性回归模型中,
来刻画回归效果,在线性回归模型中, 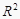 表示解释变量对于预报变量变化的贡献率
表示解释变量对于预报变量变化的贡献率 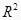 越接近1,表示回归的效果越好.
越接近1,表示回归的效果越好.
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】证明f(x)=﹣x2+3在(0,+∞)上是减函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1,x2∈[0,2]且x1≠x2时,都有
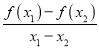 给出下列四个命题:
给出下列四个命题:①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为减函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
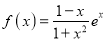 若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)计算27 +lg5﹣2log23+lg2+log29.
+lg5﹣2log23+lg2+log29.
(2)已知f(x)=3x2﹣5x+2,求f(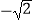 )、f(﹣a)、f(a+3).
)、f(﹣a)、f(a+3). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?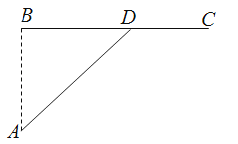
相关试题

