【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品![]() 、
、![]() ,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表:
,该所要根据该产品的研制成本、产品重量、搭载实验费用、和预计产生收益来决定具体安排.通过调查,有关数据如下表:
产品A(件) | 产品B(件) | ||
研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
参考答案:
【答案】解:设搭载产品A![]() 件,产品B y件,
件,产品B y件,
 则预计收益
则预计收益![]() .
.
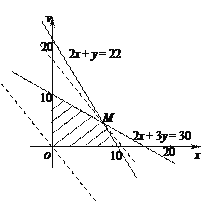
则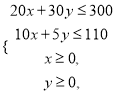 作出可行域,如图;
作出可行域,如图;
作出直线![]() 并平移.
并平移.
由图象得,当直线经过M点时, z能取得最大值,
![]() , 解得
, 解得![]() , 即
, 即![]() .
.
所以z=80×9+60×4=960(万元).
答:应搭载产品A 9件,产品B 4件,可使得利润最多达到960万元.
【解析】试题分析:设搭载A产品![]() 件,B产品
件,B产品![]() 件,依据题意得到变量x,y的线性约束条件及目标函数,然后按照线性规划求最值的步骤求解即可.但注意本题是整点问题,即一注意变量x,y的范围,二注意可行域的边界交点是否为整点.
件,依据题意得到变量x,y的线性约束条件及目标函数,然后按照线性规划求最值的步骤求解即可.但注意本题是整点问题,即一注意变量x,y的范围,二注意可行域的边界交点是否为整点.
试题解析:设搭载A产品![]() 件,B产品
件,B产品![]() 件,
件,
则总预计收益![]()
由题意知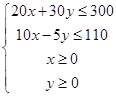 ,且
,且![]() ,
,
由此作出可行域如图所示,
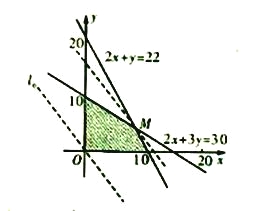
作出直线![]() 并平移,由图象知,
并平移,由图象知,
当直线经过M点时, ![]() 能取到最大值,
能取到最大值,
由![]() 解得
解得![]() 且满足
且满足![]() ,
,
即![]() 是最优解,
是最优解,
所以![]() (万元),
(万元),
答:搭载A产品9件,B产品4件,能使总预计收益达到最大值,最大预计收益为960万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油
 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Tn,且
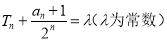 ,令cn=b2n(n∈N*),求数列{cn}的前n项和Rn.
,令cn=b2n(n∈N*),求数列{cn}的前n项和Rn. -
科目: 来源: 题型:
查看答案和解析>>【题目】某四棱锥的三视图如图所示,该四棱锥外接球的体积为( )
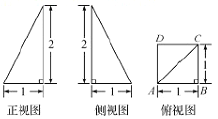
A.
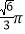 B.
B. 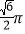 C.
C. 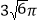 D.
D. 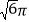
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
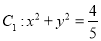 ,直线
,直线 与圆
与圆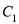 相切,且交椭圆
相切,且交椭圆 于
于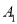 ,
, 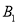 两点,
两点, 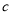 是椭圆的半焦距,
是椭圆的半焦距, 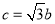 .
.(1)求
 的值;
的值;(2)
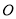 为坐标原点,若
为坐标原点,若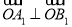 ,求椭圆
,求椭圆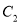 的方程;
的方程;(3)在(2)的条件下,设椭圆
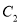 的左右顶点分别为
的左右顶点分别为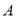 ,
,  ,动点
,动点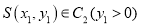 ,直线
,直线 ,
, 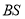 与直线
与直线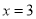 分别交于
分别交于 ,
, 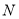 两点,求线段
两点,求线段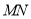 的长度的最小值.
的长度的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出四组函数,表示同一函数的是( )
A.f(x)=x﹣1,g(x)= ﹣1
﹣1
B.f(x)=2x+1,g(x)=2x﹣1
C.f(x)=|x|,g(x)=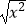
D.f(x)=1,g(x)=x0 -
科目: 来源: 题型:
查看答案和解析>>【题目】莫数学建模兴趣小组测量某移动信号塔
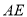 的高度
的高度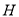 (单位:
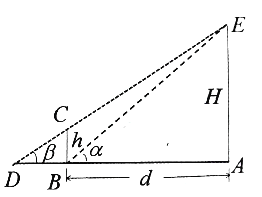
(单位: 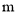 ),如图所示,垂直放置的标杆
),如图所示,垂直放置的标杆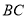 的高度
的高度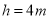 ,仰角
,仰角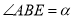 ,
, 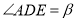 .
.
(Ⅰ)该小组已经测得一组
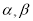 的值,
的值, 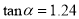 ,
, 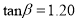 ,请推测
,请推测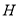 的值;
的值;(Ⅱ)该小组对测得的多组数据分析后,发现适当调节标杆到信号塔的距离
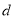 (单位:
(单位: 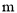 ),使得
),使得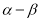 较大时,可以提高信号塔测量的精确度,若信号塔高度为
较大时,可以提高信号塔测量的精确度,若信号塔高度为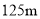 ,试问
,试问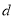 为多大时,
为多大时,  最大?
最大?
相关试题

