
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一条线段,且
上的一条线段,且![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的动点,则
上的动点,则
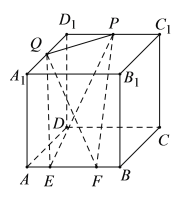
①四面体![]() 的体积为定值
的体积为定值
②直线![]() 到平面
到平面![]() 的距离为定值
的距离为定值
③点![]() 到直线
到直线![]() 的距离为定值
的距离为定值
④直线![]() 与平面
与平面![]() 所成的角为定值
所成的角为定值
其中正确结论的编号是( )
A.①②③B.①②④C.①③④D.②③④
【答案】A
【解析】
通过证明![]() 平面
平面![]() 可推出P点到平面
可推出P点到平面![]() 的距离为定值,又因为
的距离为定值,又因为![]() 为定值可判断①正确;通过证明
为定值可判断①正确;通过证明![]() 平面PEF可推出直线
平面PEF可推出直线![]() 到平面
到平面![]() 的距离为定值;由
的距离为定值;由![]() 可推出③正确;根据线面角的概念进行分析判断④.
可推出③正确;根据线面角的概念进行分析判断④.
①因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
由P是棱![]() 上的动点,故P点到平面
上的动点,故P点到平面![]() 的距离为定值,
的距离为定值,
又因为![]() 为定值,所以四面体
为定值,所以四面体![]() 的体积为定值,
的体积为定值,
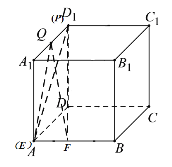
不妨取P与![]() 重合,E与A重合,此时四面体
重合,E与A重合,此时四面体![]() 的体积为
的体积为![]() ,即四面体
,即四面体![]() 的体积为定值7,①正确;
的体积为定值7,①正确;
②因为![]() AB,
AB,![]() 平面PEF,
平面PEF,![]() 平面PEF,所以
平面PEF,所以![]() 平面PEF,所以直线
平面PEF,所以直线![]() 到平面
到平面![]() 的距离为定值,
的距离为定值,
连接![]() ,过点
,过点![]() 作
作![]() 于点G,平面PEF即为平面
于点G,平面PEF即为平面![]() ,则
,则![]() 即为直线
即为直线![]() 到平面
到平面![]() 的距离,因为
的距离,因为![]() ,
,![]() ,
,
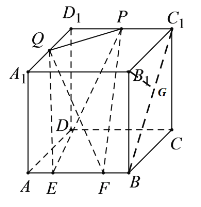
所以![]() ,
,![]() ,即直线
,即直线![]() 到平面
到平面![]() 的距离为定值
的距离为定值![]() ,②正确;
,②正确;
③因为![]() ,且点P是直线
,且点P是直线![]() 上的动点,所以点
上的动点,所以点![]() 到直线
到直线![]() 的距离为定值,
的距离为定值,![]() 即为两平行线
即为两平行线![]() 、
、![]() 之间的距离,故点
之间的距离,故点![]() 到直线
到直线![]() 的距离为定值
的距离为定值![]() ,③正确;
,③正确;
④过点P作![]() 垂直于平面QEF于点
垂直于平面QEF于点![]() ,则
,则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,
所成的角,![]() 为点P到平面
为点P到平面![]() 的距离,
的距离,![]() ,由①知
,由①知![]() ,所以
,所以![]() ,为定值,
,为定值,
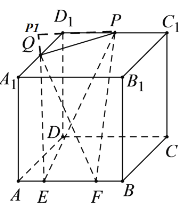
![]() ,因为点P是直线
,因为点P是直线![]() 上的动点,所以
上的动点,所以![]() 不是定值,
不是定值,
故![]() 不是定值,直线
不是定值,直线![]() 与平面
与平面![]() 所成的角不是定值,④错误.
所成的角不是定值,④错误.
故选:A


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】给出以下命题:
(1)已知回归直线方程为![]() ,样本点的中心为
,样本点的中心为![]() ,则
,则![]() ;
;
(2)已知![]() ,
,![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() 是
是![]() 的充要条件;
的充要条件;
(3)函数![]() 图象关于点
图象关于点![]() 对称且在
对称且在![]() 上单调递增;
上单调递增;
(4)命题“存在![]() ”的否定是“对于任意
”的否定是“对于任意![]() ”;
”;
(5)设函数![]() ,若函数
,若函数![]() 恰有三个零点,则实数m的取值范围为
恰有三个零点,则实数m的取值范围为![]() .
.
其中不正确的命题序号为______________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() ,
,![]() ,
,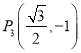 ,
,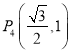 四点中恰有三点在椭圆
四点中恰有三点在椭圆![]() 上,抛物线
上,抛物线![]() 焦点到准线的距离为
焦点到准线的距离为![]() .
.
(1)求椭圆![]() 、抛物线
、抛物线![]() 的方程;
的方程;
(2)过椭圆![]() 右顶点Q的直线
右顶点Q的直线![]() 与抛物线
与抛物线![]() 交于点A、B,射线
交于点A、B,射线![]() 、
、![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() 、
、![]() .
.
(i)证明:![]() 为定值;
为定值;
(ii)记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小1.
的距离小1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生活超市有一专柜预代理销售甲乙两家公司的一种可相互替代的日常生活用品.经过一段时间分别单独试销甲乙两家公司的商品,从销售数据中随机各抽取50天,统计每日的销售数量,得到如下的频数分布条形图.甲乙两家公司给该超市的日利润方案为:甲公司给超市每天基本费用为90元,另外每销售一件提成1元;乙公司给超市每天的基本费用为130元,每日销售数量不超过83件没有提成,超过83件的部分每件提成10元.
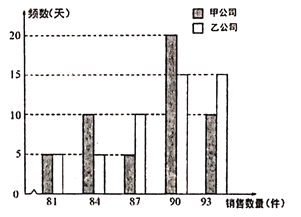
(Ⅰ)求乙公司给超市的日利润![]() (单位:元)与日销售数量
(单位:元)与日销售数量![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
(1)求甲公司产品销售数量不超过87件的概率;
(2)如果仅从日均利润的角度考虑,请你利用所学过的统计学知识为超市作出抉择,选择哪家公司的产品进行销售?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() :
:![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若![]() ,求直线的方程;
,求直线的方程;
(2)过点![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,若线段
两点,若线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求点
,求点![]() 到直线
到直线![]() 与
与![]() 距离和的最大值.
距离和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把方程![]() 表示的曲线作为函数
表示的曲线作为函数![]() 的图象,则下列结论正确的是( )
的图象,则下列结论正确的是( )
①![]() 在R上单调递减
在R上单调递减
②![]() 的图像关于原点对称
的图像关于原点对称
③![]() 的图象上的点到坐标原点的距离的最小值为3
的图象上的点到坐标原点的距离的最小值为3
④函数![]() 不存在零点
不存在零点
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com