【题目】已知函数f(x)=(x﹣ ![]() )e﹣x(x≥
)e﹣x(x≥ ![]() ).
).
(Ⅰ)求f(x)的导函数;
(Ⅱ)求f(x)在区间[ ![]() ,+∞)上的取值范围.
,+∞)上的取值范围.
参考答案:
【答案】解:(Ⅰ)函数f(x)=(x﹣ ![]() )e﹣x(x≥
)e﹣x(x≥ ![]() ),
),
导数f′(x)=(1﹣ ![]()
![]() 2)e﹣x﹣(x﹣
2)e﹣x﹣(x﹣ ![]() )e﹣x
)e﹣x
=(1﹣x+ ![]() )e﹣x=(1﹣x)(1﹣
)e﹣x=(1﹣x)(1﹣ ![]() )e﹣x;
)e﹣x;
(Ⅱ)由f(x)的导数f′(x)=(1﹣x)(1﹣ ![]() )e﹣x ,
)e﹣x ,
可得f′(x)=0时,x=1或 ![]() ,
,
当 ![]() <x<1时,f′(x)<0,f(x)递减;
<x<1时,f′(x)<0,f(x)递减;
当1<x< ![]() 时,f′(x)>0,f(x)递增;
时,f′(x)>0,f(x)递增;
当x> ![]() 时,f′(x)<0,f(x)递减,
时,f′(x)<0,f(x)递减,
且x≥ ![]() x2≥2x﹣1(x﹣1)2≥0,
x2≥2x﹣1(x﹣1)2≥0,
则f(x)≥0.
由f( ![]() )=
)= ![]() e
e ![]() ,f(1)=0,f(
,f(1)=0,f( ![]() )=
)= ![]() e
e ![]() ,
,
即有f(x)的最大值为 ![]() e
e ![]() ,最小值为f(1)=0.
,最小值为f(1)=0.
则f(x)在区间[ ![]() ,+∞)上的取值范围是[0,
,+∞)上的取值范围是[0, ![]() e
e ![]() ].
].
【解析】(Ⅰ)求出f(x)的导数,注意运用复合函数的求导法则,即可得到所求;
(Ⅱ)求出f(x)的导数,求得极值点,讨论当 ![]() <x<1时,当1<x<
<x<1时,当1<x< ![]() 时,当x>
时,当x> ![]() 时,f(x)的单调性,判断f(x)≥0,计算f(
时,f(x)的单调性,判断f(x)≥0,计算f( ![]() ),f(1),f(
),f(1),f( ![]() ),即可得到所求取值范围.
),即可得到所求取值范围.
【考点精析】本题主要考查了简单复合函数的导数和利用导数研究函数的单调性的相关知识点,需要掌握复合函数求导:![]() 和
和![]() ,称则
,称则![]() 可以表示成为
可以表示成为![]() 的函数,即
的函数,即![]() 为一个复合函数
为一个复合函数![]() ;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间
;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 的公差不为零,
的公差不为零, ,且
,且 成等比数列.
成等比数列.(1)求
 的通项公式;
的通项公式;(2)求
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中, 分别是
分别是 的中点,
的中点,


(1) 求证:
 平面
平面 ;
;(2) 求异面直线
 与
与 所成角的余弦值;
所成角的余弦值;(3) 求点
 到平面
到平面 的距离。
的距离。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线x2=y,点A(﹣
 ,
,  ),B(
),B(  ,
,  ),抛物线上的点P(x,y)(﹣
),抛物线上的点P(x,y)(﹣  <x<
<x<  ),过点B作直线AP的垂线,垂足为Q.
),过点B作直线AP的垂线,垂足为Q.
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求|PA||PQ|的最大值.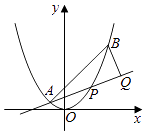
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱中,AB=2,由顶点B沿棱柱侧面经过棱
 到顶点C1的最短路线与棱
到顶点C1的最短路线与棱 的交点记为M,求:
的交点记为M,求: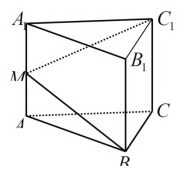
(Ⅰ)三棱柱的侧面展开图的对角线长.
(Ⅱ)该最短路线的长及
 的值.
的值.(Ⅲ)平面
 与平面ABC所成二面角(锐二面角)
与平面ABC所成二面角(锐二面角) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,
, 是不共面的三个向量,则能构成一个基底的一组向量是( )
是不共面的三个向量,则能构成一个基底的一组向量是( )A. 2
 ,
, ﹣
﹣ ,
, +2
+2 B. 2
B. 2 ,
, ﹣
﹣ ,
, +2
+2
C.
 ,2
,2 ,
, ﹣
﹣ D.
D.  ,
, +
+ ,
, ﹣
﹣
相关试题

