【题目】已知![]() ,
,![]() ,
,![]() 是不共面的三个向量,则能构成一个基底的一组向量是( )
是不共面的三个向量,则能构成一个基底的一组向量是( )
A. 2![]() ,
,![]() ﹣
﹣![]() ,
,![]() +2
+2![]() B. 2
B. 2![]() ,
,![]() ﹣
﹣![]() ,
,![]() +2
+2![]()
C. ![]() ,2
,2![]() ,
,![]() ﹣
﹣![]() D.
D. ![]() ,
,![]() +
+![]() ,
,![]() ﹣
﹣![]()
参考答案:
【答案】C
【解析】
根据空间向量基本定理,空间不共面的三个向量可以作为一个基底.由此结合向量共面的充要条件,对各个选项依次加以判断,即可得到本题答案.
对于A,因为2![]() =
=![]() (
(![]() ﹣
﹣![]() )+
)+![]() (
(![]() +2
+2![]() ),得2
),得2![]() 、
、![]() ﹣
﹣![]() 、
、![]() +2
+2![]() 三个向量共面,故它们不能构成一个基底,A不正确;
三个向量共面,故它们不能构成一个基底,A不正确;
对于B,因为2![]() =
=![]() (
(![]() ﹣
﹣![]() )+
)+![]() (
(![]() +2
+2![]() ),得2
),得2![]() 、
、![]() ﹣
﹣![]() 、
、![]() +2
+2![]() 三个向量共面,故它们不能构成一个基底,B不正确;
三个向量共面,故它们不能构成一个基底,B不正确;
对于C,因为找不到实数λ、μ,使![]() =λ2
=λ2![]() +μ(
+μ(![]() ﹣
﹣![]() )成立,故
)成立,故![]() 、2
、2![]() 、
、![]() ﹣
﹣![]() 三个向量不共面,
三个向量不共面,
它们能构成一个基底,C正确;
对于D,因为![]() =
=![]() (
(![]() +
+![]() )﹣
)﹣![]() (
(![]() ﹣
﹣![]() ),得
),得![]() 、
、![]() +
+![]() 、
、![]() ﹣
﹣![]() 三个向量共面,故它们不能构成一个基底,D不正确
三个向量共面,故它们不能构成一个基底,D不正确
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣
 )e﹣x(x≥
)e﹣x(x≥  ).
).
(Ⅰ)求f(x)的导函数;
(Ⅱ)求f(x)在区间[ ,+∞)上的取值范围.
,+∞)上的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线x2=y,点A(﹣
 ,
,  ),B(
),B(  ,
,  ),抛物线上的点P(x,y)(﹣
),抛物线上的点P(x,y)(﹣  <x<
<x<  ),过点B作直线AP的垂线,垂足为Q.
),过点B作直线AP的垂线,垂足为Q.
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求|PA||PQ|的最大值.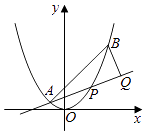
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱中,AB=2,由顶点B沿棱柱侧面经过棱
 到顶点C1的最短路线与棱
到顶点C1的最短路线与棱 的交点记为M,求:
的交点记为M,求: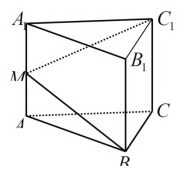
(Ⅰ)三棱柱的侧面展开图的对角线长.
(Ⅱ)该最短路线的长及
 的值.
的值.(Ⅲ)平面
 与平面ABC所成二面角(锐二面角)
与平面ABC所成二面角(锐二面角) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD
 中,以D为原点建立空间直角坐标系,E为B
中,以D为原点建立空间直角坐标系,E为B 的中点,F为
的中点,F为 的中点,则下列向量中,能作为平面AEF的法向量的是( )
的中点,则下列向量中,能作为平面AEF的法向量的是( )
A. (1,-2,4) B. (-4,1,-2)
C. (2,-2,1) D. (1,2,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体ABCD
 中,下面结论错误的是( )
中,下面结论错误的是( )
A. BD∥平面C
 B. AC1⊥BD
B. AC1⊥BDC. AC1⊥平面C
 D. 向量
D. 向量 与
与 的夹角为60°
的夹角为60° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱ABC﹣A1B1C1中,所有棱长均为1,则点B1到平面ABC1的距离为 .

相关试题

