【题目】已知等差数列![]() 的公差不为零,
的公差不为零,![]() ,且
,且![]() 成等比数列.
成等比数列.
(1)求![]() 的通项公式;
的通项公式;
(2)求![]() .
.
参考答案:
【答案】(1)![]() (1)Sn=-3n2+28n
(1)Sn=-3n2+28n
【解析】
(1)设等差数列{an}的公差为d≠0,利用成等比数列的定义可得,a112=a1a1,再利用等差数列的通项公式可得(a1+10d)2=a1(a1+12d),化为d(2a1+25d)=0,解出d即可得到通项公式an;
(2)由(1)可得a3n-2=-2(3n-2)+27=-6n+31,可知此数列是以25为首项,-6为公差的等差数列.利用等差数列的前n项和公式即可得出a1+a4+a7+…+a3n-2.
(1)设{an}的公差为d.由题意,a112=a1a13,即(a1+10d)2=a1(a1+12d).
于是d(2a1+25d)=0.又a1=25,所以d=0(舍去),d=-2.故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.
由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.
从而Sn=![]() (a1+a3n-2)=
(a1+a3n-2)=![]() (-6n+56)=-3n2+28n.
(-6n+56)=-3n2+28n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,若
中,若 ,则这三角形一定是( )
,则这三角形一定是( )A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰或直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin2x﹣cos2x﹣2
 sinx cosx(x∈R).
sinx cosx(x∈R).
(Ⅰ)求f( )的值.
)的值.
(Ⅱ)求f(x)的最小正周期及单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,
中, 分别是
分别是 的中点,
的中点,


(1) 求证:
 平面
平面 ;
;(2) 求异面直线
 与
与 所成角的余弦值;
所成角的余弦值;(3) 求点
 到平面
到平面 的距离。
的距离。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣
 )e﹣x(x≥
)e﹣x(x≥  ).
).
(Ⅰ)求f(x)的导函数;
(Ⅱ)求f(x)在区间[ ,+∞)上的取值范围.
,+∞)上的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线x2=y,点A(﹣
 ,
,  ),B(
),B(  ,
,  ),抛物线上的点P(x,y)(﹣
),抛物线上的点P(x,y)(﹣  <x<
<x<  ),过点B作直线AP的垂线,垂足为Q.
),过点B作直线AP的垂线,垂足为Q.
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求|PA||PQ|的最大值.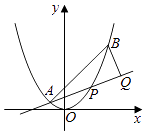
相关试题

