【题目】已知直线: ![]() (
(![]() 为给定的正常数,
为给定的正常数, ![]() 为参数,
为参数, ![]() )构成的集合为
)构成的集合为![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时, ![]() 中直线的斜率为
中直线的斜率为![]() ;
;
②![]() 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.
③当![]() 时,存在某个定点,该定点到
时,存在某个定点,该定点到![]() 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当![]() 时,
时, ![]() 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为![]() ;
;
其中正确的是__________(写出所有正确命题的编号).
参考答案:
【答案】③④
【解析】①当![]() 时,
时, ![]() ,
, ![]() 中直线的斜率为
中直线的斜率为![]() ,故不正确;
,故不正确;
②根据![]() ,可知
,可知![]() 中所有直线不可能经过一个定点,不正确;
中所有直线不可能经过一个定点,不正确;
③当![]() 时,方程为
时,方程为![]() ,存在定点
,存在定点![]() ,该定点到
,该定点到![]() 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④因为![]() 既满足直线
既满足直线![]() 的方程,
的方程,
也满足椭圆![]() 的方程,且把直线
的方程,且把直线![]() 的方程代入椭圆
的方程代入椭圆![]()
的方程可得![]() ,当
,当![]() 时,
时, ![]() 为椭圆的切线,
为椭圆的切线,
当![]() 中两直线分别与椭圆相切于短轴两端点时,
中两直线分别与椭圆相切于短轴两端点时,
它们间的距离为![]() ,即为最小距离,即最小值为
,即为最小距离,即最小值为![]() ,故④正确.
,故④正确.
故答案为:③④.
-
科目: 来源: 题型:
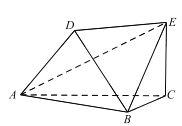
查看答案和解析>>【题目】如图,以
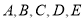 为顶点的六面体中,
为顶点的六面体中, 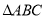 和
和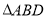 均为等边三角形,且平面
均为等边三角形,且平面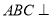 平面
平面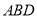 ,
, 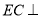 平面
平面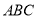 ,
, 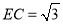 ,
, 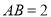 .
.
(1)求证:
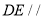 平面
平面 ;
;(2)求此六面体的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
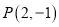 ,求:
,求:(Ⅰ)过
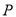 点与原点距离为2的直线
点与原点距离为2的直线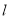 的方程;
的方程;(Ⅱ)过
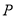 点与原点距离最大的直线
点与原点距离最大的直线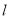 的方程,最大距离是多少?
的方程,最大距离是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗
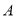 原料1千克、
原料1千克、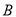 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗 原料2千克,
原料2千克, 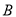 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗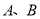 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
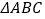 中,角
中,角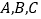 所对的边分别为
所对的边分别为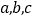 ,已知
,已知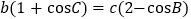 .
.(1)求证:
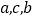 成等差数列;
成等差数列;(2)若
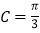 ,
,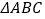 的面积为
的面积为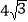 ,求
,求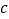 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
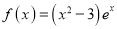 ,设关于
,设关于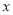 的方程
的方程 有
有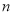 个不同的实数解,则
个不同的实数解,则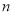 的所有可能的值为( )
的所有可能的值为( )A. 3 B. 1或3 C. 4或6 D. 3或4或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的直角坐标方程;
的直角坐标方程;(2)已知点
 的直角坐标为
的直角坐标为 ,直线
,直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点 ,求
,求 的取值范围.
的取值范围.
相关试题

