【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,底面
,底面![]() 为长方形,且
为长方形,且![]() ,
,![]() 是
是![]() 的中点,作
的中点,作![]() 交
交![]() 于点
于点![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在(2)的条件下,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)推导出![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,进而
,进而![]() ,再证出
,再证出![]() ,从而
,从而![]() 平面
平面![]() ,
,![]() ,再由
,再由![]() ,能证明
,能证明![]() 平面
平面![]() .
.
(2)由![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系![]() ,利用向量法能求出直线
,利用向量法能求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(3)求出平面![]() 的法向量和平面PBC的法向量,利用向量法能求出二面角D-BP-C的余弦值.
的法向量和平面PBC的法向量,利用向量法能求出二面角D-BP-C的余弦值.
详解:
(1)证明:∵![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
由于底面![]() 为长方形,∴
为长方形,∴![]() ,而
,而![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由题意易知![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,建立如图空间直角坐标系
为坐标原点,建立如图空间直角坐标系![]() ,可得
,可得![]() ,
,
设![]() ,则有
,则有![]() ,∴
,∴![]()
∴![]() ,
,
∴![]() ,
,![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,且由(1)知
,且由(1)知![]() 为平面
为平面![]() 的法向量
的法向量
∴![]()
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)由(2)知![]() ,
,![]() ,
,![]()
设平面![]() 的法向量
的法向量![]() ,由
,由![]() ,则
,则![]()
令![]() ,则
,则![]() ,
,
∴![]()
由(1)![]() 平面
平面![]() ,
,
∴![]() 为平面PBC的法向量,
为平面PBC的法向量,![]()
设二面角![]() 为
为![]() ,则
,则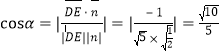
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是
 的中点.
的中点.
(1)设P是
 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AD⊥平面PCD,PD⊥CD,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2AB,
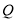 为棱PC上一点.
为棱PC上一点.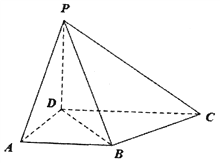
(Ⅰ)若点
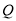 是PC的中点,证明:B
是PC的中点,证明:B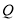 ∥平面PAD;
∥平面PAD;(Ⅱ)
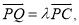 试确定
试确定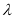 的值使得二面角
的值使得二面角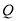 -BD-P为60°.
-BD-P为60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果
 ,并且
,并且 ,那么下列不等式中不一定成立的是( )
,那么下列不等式中不一定成立的是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由矩形
 和菱形
和菱形 组成的一个平面图形,其中
组成的一个平面图形,其中 ,
,  ,将其沿
,将其沿 折起使得
折起使得 与
与 重合,连结
重合,连结 ,如图2.
,如图2.(1)证明图2中的
 四点共面,且平面
四点共面,且平面 平面
平面 ;
;(2)求图2中的四边形
 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在空间中,给出下列说法:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面
 内有不共线的三点到平面
内有不共线的三点到平面 的距离相等,则
的距离相等,则 ;④过平面
;④过平面 的一条斜线,有且只有一个平面与平面
的一条斜线,有且只有一个平面与平面 垂直.其中正确的是( )
垂直.其中正确的是( )A. ①③B. ②④C. ①④D. ②③
相关试题

