【题目】如图,在四棱锥P-ABCD中,AD⊥平面PCD,PD⊥CD,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2AB, ![]() 为棱PC上一点.
为棱PC上一点.
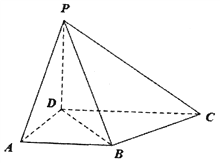
(Ⅰ)若点![]() 是PC的中点,证明:B
是PC的中点,证明:B![]() ∥平面PAD;
∥平面PAD;
(Ⅱ) ![]() 试确定
试确定![]() 的值使得二面角
的值使得二面角![]() -BD-P为60°.
-BD-P为60°.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ) ![]()
【解析】试题分析:(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由三角形中位线定理结合可得题设条件可得四边形
,由三角形中位线定理结合可得题设条件可得四边形![]() 是平行四边形,
是平行四边形, ![]()
![]() ,由线面平行的判定定理可得结论;(Ⅱ)
,由线面平行的判定定理可得结论;(Ⅱ) ![]() 两两垂直,以
两两垂直,以![]() 为原点
为原点![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,可证明
轴建立空间直角坐标系,可证明![]() 平面
平面![]() ,
, ![]() 是平面
是平面![]() 的法向量,利用向量垂直数量积为零,用
的法向量,利用向量垂直数量积为零,用![]() 表示出平面
表示出平面![]() 的法向量,利用空间向量夹角余弦公式列方程求解即可.
的法向量,利用空间向量夹角余弦公式列方程求解即可.
试题解析:(Ⅰ)取PD的中点M,连接AM,M![]() ,
,
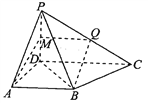
![]() ,
,
![]() M
M![]() ∥CD,
∥CD, ![]()
又AB∥CD, ![]() ∥AB,QM=AB,
∥AB,QM=AB,
则四边形ABQM是平行四边形. ![]() ∥AM.
∥AM.
又![]() 平面PAD,BQ
平面PAD,BQ![]() 平面PAD,
平面PAD, ![]() ∥平面PAD.
∥平面PAD.
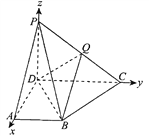
(Ⅱ)解:由题意可得DA,DC,DP两两垂直,以D为原点,DA,DC,DP所在直线为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
则P(0,1,1),C(0,2,0),A(1,0,0),B(1,1,0).
令![]()
![]()
![]()
又易证BC⊥平面PBD, ![]()
设平面QBD的法向量为![]()
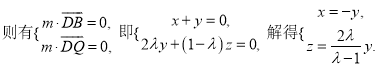
令![]()
![]() ,
,
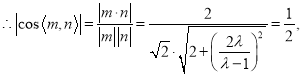
解得![]()
![]() Q在棱PC上,
Q在棱PC上, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)求
 的定义域;
的定义域;(2)判断
 的奇偶性并给予证明;
的奇偶性并给予证明;(3)求关于x的不等式
 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
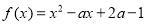 (
(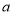 为实常数).
为实常数).
(1)当
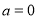 时,作出
时,作出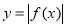 的图象,并写出它的单调递增区间;
的图象,并写出它的单调递增区间;(2)设
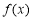 在区间
在区间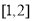 的最小值为
的最小值为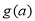 ,求
,求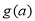 的表达式;
的表达式;(3)已知函数
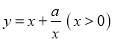 在
在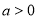 的情况下:其在区间
的情况下:其在区间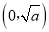 单调递减,在区间
单调递减,在区间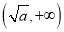 单调递增.设
单调递增.设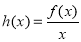 ,若函数
,若函数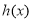 在区间
在区间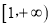 上是增函数,求实数
上是增函数,求实数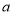 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是
 的中点.
的中点.
(1)设P是
 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果
 ,并且
,并且 ,那么下列不等式中不一定成立的是( )
,那么下列不等式中不一定成立的是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 为长方形,且
为长方形,且 ,
,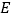 是
是 的中点,作
的中点,作 交
交 于点
于点 .
.
(1)证明:
 平面
平面 ;
;(2)若三棱锥
 的体积为
的体积为 ,求直线
,求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)在(2)的条件下,求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由矩形
 和菱形
和菱形 组成的一个平面图形,其中
组成的一个平面图形,其中 ,
,  ,将其沿
,将其沿 折起使得
折起使得 与
与 重合,连结
重合,连结 ,如图2.
,如图2.(1)证明图2中的
 四点共面,且平面
四点共面,且平面 平面
平面 ;
;(2)求图2中的四边形
 的面积.
的面积.
相关试题

