【题目】据市场分析,某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本![]() (万元)可以看成月产量
(万元)可以看成月产量![]() (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本![]() (万元)关于月产量
(万元)关于月产量![]() (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品的销售价为每吨1.6万元,那么月产量为多少时,可获最大利润.
(3)当月产量为多少吨时,每吨平均成本最低,最低成本是多少万元?
参考答案:
【答案】(1)![]() ;(2)月产量为23吨时,可获最大利润12.9万元;(3)月产量为20吨时,每吨平均成本最低,最低成本为1万元.
;(2)月产量为23吨时,可获最大利润12.9万元;(3)月产量为20吨时,每吨平均成本最低,最低成本为1万元.
【解析】试题分析:(1)设出函数的表达式,代入数据,通过待定系数法求即可;(2)写出利润函数,利用二次函数求最值,来求利润的最大值;(3)写出每吨的成本函数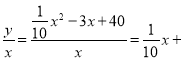
![]() ,利用均值不等式求最值即可.
,利用均值不等式求最值即可.
试题解析:(1)设![]()
将![]() ,
, ![]() 代入上式得,
代入上式得, ![]() ,解得
,解得![]()
∴![]()
(2)设利润为![]() ,则
,则![]()
![]()
![]()
因为![]() ,
,
所以月产量为23吨时,可获最大利润12.9万元
(3)
![]()
当且仅当![]() ,即
,即![]() 时上式“=”成立.
时上式“=”成立.
故当月产量为20吨时,每吨平均成本最低,最低成本为1万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为
 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为 。
。(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
(Ⅰ)求证:AB⊥平面ADC;
(Ⅱ)若AD=2,直线CA与平面ABD所成角的正弦值为
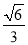 ,求二面角E-AD-C的余弦值.
,求二面角E-AD-C的余弦值.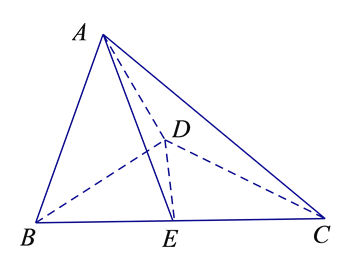
-
科目: 来源: 题型:
查看答案和解析>>【题目】设各项均为正数的数列
 的前
的前 项和为
项和为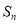 ,满足
,满足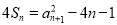 ,且
,且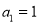 ,公比大于1的等比数列
,公比大于1的等比数列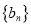 满足
满足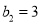 ,
, 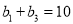 .
.(1)求证数列
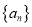 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;(2)若
 ,求数列
,求数列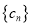 的前
的前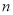 项和
项和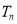 ;
;(3)在(2)的条件下,若
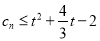 对一切正整数
对一切正整数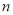 恒成立,求实数
恒成立,求实数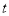 的取值
的取值 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)已知
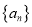 是公差不为零的等差数列,
是公差不为零的等差数列, 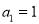 ,且
,且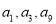 成等比数列.
成等比数列.(1)求数列
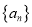 的通项;
的通项;(2)求数列
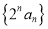 的前n项和.
的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,函数
,函数 .
.(Ⅰ)讨论函数
 的单调性;
的单调性;(Ⅱ)若函数
 有两个相异零点
有两个相异零点 ,
,  ,求证:
,求证:  .(其中e为自然对数的底数)
.(其中e为自然对数的底数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙
 :
:  与⊙
与⊙ :
:  ,以
,以 ,
,  分别为左右焦点的椭圆
分别为左右焦点的椭圆 :
:  经过两圆的交点.
经过两圆的交点.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)
 ,
,  分别为椭圆
分别为椭圆 的左右顶点,
的左右顶点,  ,
,  ,
,  是椭圆
是椭圆 上非顶点的三点,若
上非顶点的三点,若 ∥
∥ ,
,  ∥
∥ ,试问
,试问 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
相关试题

