【题目】如图,在直三棱柱![]() 中,
中, ![]() 是线段
是线段![]() 上一点.
上一点.
点.
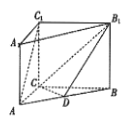
(1)确定![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,设二面角
,设二面角![]() 的大小为
的大小为![]() ,求证:
,求证: ![]()
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)当![]() 时,可证明
时,可证明![]() 平面
平面![]() ,再根据平面几何知识求解即可;(2)以
,再根据平面几何知识求解即可;(2)以![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,求出平面
轴建立如图所示的空间直角坐标系,求出平面![]() 的一个法向量及平面
的一个法向量及平面![]() 的一个法向量,利用空间向量夹角余弦公式可得结果.
的一个法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)当![]() 时,∵
时,∵![]() ,∴由射影定理得
,∴由射影定理得![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴当
,∴当![]() 时,平面
时,平面![]() 平面
平面![]() .
.
(2)以![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
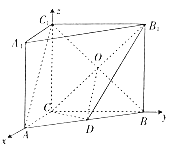
则![]() ,
, ![]() ,
, ![]() .
.
连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点.
的中点.
∵平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 为
为![]() 的中点.
的中点.
∴![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,且
,且![]() ,
,
令![]() ,可取平面
,可取平面![]() 的一个法向量
的一个法向量![]() ,
,
而平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴![]() ,∵二面角
,∵二面角![]() 为锐角,
为锐角,
∴![]() ,又
,又![]() ,∴
,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】是否存在常数
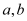 ,使等式
,使等式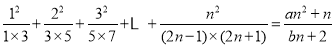 对于一切
对于一切 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明? -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
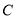 的参数方程:
的参数方程: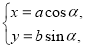 (
(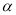 为参数),曲线
为参数),曲线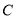 上的点
上的点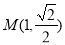 对应的参数
对应的参数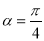 .以坐标原点
.以坐标原点 为极点,以
为极点,以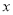 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点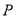 的极坐标是
的极坐标是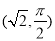 ,直线
,直线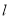 过点
过点 ,且与曲线
,且与曲线 交于不同的两点
交于不同的两点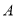 ,
,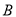 .
.(1)求曲线
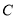 的普通方程;
的普通方程;(2)求
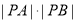 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小波从
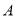 街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是
街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是 ,红灯亮的概率都是
,红灯亮的概率都是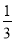 .
.(1)求小波遇到4次绿灯后,处于
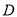 街区的概率;
街区的概率;(2)若小波一共遇到了3次红绿灯,设此时小波所处的街区与
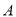 街区相距的街道数为
街区相距的街道数为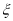 (如小波若处在
(如小波若处在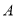 街区则相距零个街道,处在
街区则相距零个街道,处在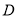 ,
,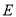 街区都是相距2个街道),求
街区都是相距2个街道),求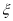 的分布列和数学期望.
的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数列
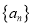 满足
满足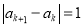 (
(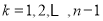 ;
; 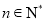 ,
, 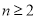 ),称数列
),称数列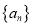 为
为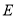 数列,记
数列,记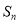 为其前
为其前 项和.
项和.(Ⅰ)写出一个满足
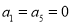 ,且
,且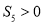 的
的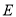 数列
数列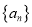 ;
;(Ⅱ)若
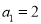 ,
, 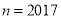 ,证明:若
,证明:若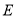 数列
数列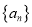 是递增数列,则
是递增数列,则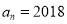 ;反之,若
;反之,若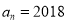 ,则
,则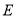 数列
数列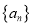 是递增数列;
是递增数列;(Ⅲ)对任意给定的整数
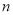 (
(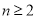 ),是否存在首项为0的
),是否存在首项为0的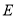 数列
数列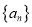 ,使得
,使得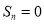 ?如果存在,写出一个满足条件的
?如果存在,写出一个满足条件的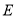 数列
数列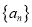 ;如果不存在,说明理由.
;如果不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 满足:①圆心在第一象限,截
满足:①圆心在第一象限,截 轴所得弦长为2;②被
轴所得弦长为2;②被 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为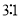 ;③圆心到直线
;③圆心到直线 的距离为
的距离为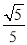 .
.(Ⅰ)求圆
 的方程;
的方程;(Ⅱ)若点
 是直线
是直线 上的动点,过点
上的动点,过点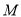 分别做圆
分别做圆 的两条切线,切点分别为
的两条切线,切点分别为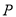 ,
,  ,求证:直线
,求证:直线 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
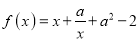 ,
, 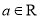 .
.(Ⅰ)若
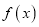 是奇函数,且在区间
是奇函数,且在区间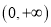 上是增函数,求
上是增函数,求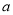 的值;
的值;(Ⅱ)设
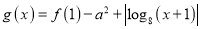 ,若
,若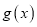 在区间
在区间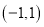 内有两个不同的零点
内有两个不同的零点 ,
, 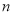 ,求
,求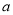 的取值范围,并求
的取值范围,并求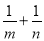 的值.
的值.
相关试题

