【题目】若数列![]() 满足
满足![]() (
(![]() ;
; ![]() ,
, ![]() ),称数列
),称数列![]() 为
为![]() 数列,记
数列,记![]() 为其前
为其前![]() 项和.
项和.
(Ⅰ)写出一个满足![]() ,且
,且![]() 的
的![]() 数列
数列![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,证明:若
,证明:若![]() 数列
数列![]() 是递增数列,则
是递增数列,则![]() ;反之,若
;反之,若![]() ,则
,则![]() 数列
数列![]() 是递增数列;
是递增数列;
(Ⅲ)对任意给定的整数![]() (
(![]() ),是否存在首项为0的
),是否存在首项为0的![]() 数列
数列![]() ,使得
,使得![]() ?如果存在,写出一个满足条件的
?如果存在,写出一个满足条件的![]() 数列
数列![]() ;如果不存在,说明理由.
;如果不存在,说明理由.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)证明见解析(Ⅲ)见解析
(Ⅱ)证明见解析(Ⅲ)见解析
【解析】试题分析:(Ⅰ)由题![]() 是一个满足条件的
是一个满足条件的![]() 数列{
数列{![]() .
.
(Ⅱ)若![]() 数列{
数列{![]() 是递增数列,则
是递增数列,则![]() ,推导出{
,推导出{![]() 是首项为2,公差为1的等差数列,从而得到
是首项为2,公差为1的等差数列,从而得到![]() ;反之,若
;反之,若![]() ,由
,由![]() (当且仅当
(当且仅当![]() 时,等号成立),推导出E数列{
时,等号成立),推导出E数列{![]() 是递增数列.(Ⅲ)
是递增数列.(Ⅲ) ![]() 即
即![]() ,知
,知![]() 数列{
数列{![]() 中相邻两项
中相邻两项![]() 奇偶性相反,即
奇偶性相反,即![]() 为偶数
为偶数![]() 为奇数,由此利用分类讨论思想能求出结果.
为奇数,由此利用分类讨论思想能求出结果.
试题解析:(Ⅰ)0,1,2,1,0是一个满足条件的![]() 数列
数列![]() .
.
(答案不唯一,0,1,0,1,0也是一个满足条件的![]() 数列
数列![]() )
)
(Ⅱ)若![]() 数列
数列![]() 是递增数列,则
是递增数列,则![]() (
(![]() ),
),
所以![]() 是首项为2,公差为1的等差数列.
是首项为2,公差为1的等差数列.
故![]() .
.
反之,若![]() ,由于
,由于![]() (等号成立当且仅当
(等号成立当且仅当![]() ),
),
所以![]()
![]()
即对![]() ,恒有
,恒有![]() ,故
,故![]() 数列
数列![]() 是递增数列.
是递增数列.
(Ⅲ)由![]() 即
即![]() ,知
,知![]() 数列
数列![]() 中相邻两项
中相邻两项![]() 、
、![]() 奇偶性相反,即
奇偶性相反,即![]() ,
, ![]() ,
, ![]() ,……为偶数,
,……为偶数, ![]() ,
, ![]() ,
, ![]() ,……为奇数.
,……为奇数.
①当![]() (
(![]() )时,存在首项为0的
)时,存在首项为0的![]() 数列
数列![]() ,使得
,使得![]() .
.
例如,构造![]() :
: ![]() ,…,
,…, ![]() ,…,
,…, ![]() ,其中
,其中![]() ,
,
![]() ,
, ![]() ,
, ![]() (
(![]() )
)
②当![]() (
(![]() )时,也存在首项为0的
)时,也存在首项为0的![]() 数列
数列![]() ,使得
,使得![]() .
.
例如,构造![]() :
: ![]() ,…,
,…, ![]() ,…,
,…, ![]() ,
,
其中![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ),
),![]() .
.
③当![]() 或
或![]() (
(![]() )时,数列
)时,数列![]() 中偶数项
中偶数项![]() ,
, ![]() ,
, ![]() ,……共有
,……共有![]() 奇数项,且
奇数项,且![]() ,
, ![]() ,
, ![]() ,……均为奇数,所以和
,……均为奇数,所以和![]() 为奇数.
为奇数.
又和![]() 为偶数,因此
为偶数,因此![]() 为奇数即
为奇数即![]() .
.
此时,满足条件的![]() 数列
数列![]() 不存在.
不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
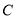 的参数方程:
的参数方程: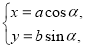 (
(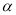 为参数),曲线
为参数),曲线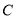 上的点
上的点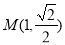 对应的参数
对应的参数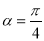 .以坐标原点
.以坐标原点 为极点,以
为极点,以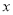 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点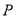 的极坐标是
的极坐标是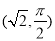 ,直线
,直线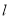 过点
过点 ,且与曲线
,且与曲线 交于不同的两点
交于不同的两点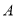 ,
,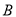 .
.(1)求曲线
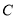 的普通方程;
的普通方程;(2)求
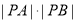 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小波从
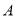 街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是
街区开始向右走,在每个十字路口都会遇到红绿灯,要是遇到绿灯则小波继续往前走,遇到红灯就往回走,假设任意两个十字路口的绿灯亮或红灯亮都是相互独立的,且绿灯亮的概率都是 ,红灯亮的概率都是
,红灯亮的概率都是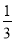 .
.(1)求小波遇到4次绿灯后,处于
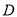 街区的概率;
街区的概率;(2)若小波一共遇到了3次红绿灯,设此时小波所处的街区与
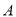 街区相距的街道数为
街区相距的街道数为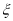 (如小波若处在
(如小波若处在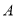 街区则相距零个街道,处在
街区则相距零个街道,处在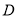 ,
,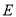 街区都是相距2个街道),求
街区都是相距2个街道),求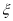 的分布列和数学期望.
的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
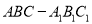 中,
中, 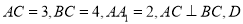 是线段
是线段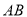 上一点.
上一点.点.
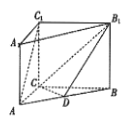
(1)确定
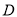 的位置,使得平面
的位置,使得平面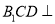 平面
平面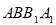 ;
;(2)若
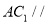 平面
平面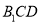 ,设二面角
,设二面角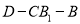 的大小为
的大小为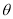 ,求证:
,求证: 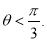
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 满足:①圆心在第一象限,截
满足:①圆心在第一象限,截 轴所得弦长为2;②被
轴所得弦长为2;②被 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为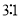 ;③圆心到直线
;③圆心到直线 的距离为
的距离为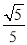 .
.(Ⅰ)求圆
 的方程;
的方程;(Ⅱ)若点
 是直线
是直线 上的动点,过点
上的动点,过点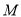 分别做圆
分别做圆 的两条切线,切点分别为
的两条切线,切点分别为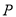 ,
,  ,求证:直线
,求证:直线 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
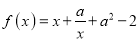 ,
, 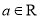 .
.(Ⅰ)若
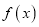 是奇函数,且在区间
是奇函数,且在区间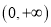 上是增函数,求
上是增函数,求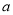 的值;
的值;(Ⅱ)设
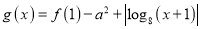 ,若
,若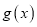 在区间
在区间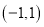 内有两个不同的零点
内有两个不同的零点 ,
, 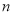 ,求
,求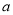 的取值范围,并求
的取值范围,并求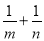 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
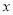 (单位:千元)对年利润
(单位:千元)对年利润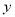 (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费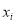 和年利润
和年利润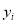 (
(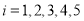 )进行了统计,列出了下表:
)进行了统计,列出了下表: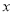 (单位:千元)
(单位:千元)2
4
7
17
30
 (单位:万元)
(单位:万元)1
2
3
4
5
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合
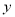 与
与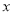 的关系,请你帮助建立
的关系,请你帮助建立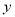 关于
关于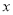 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)(2)小李决定选择对数回归模型拟合
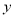 与
与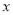 的关系,得到了回归方程:
的关系,得到了回归方程: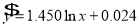 ,并提供了相关指数
,并提供了相关指数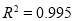 .请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析分析数据
.请用相关指数说明选择哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析分析数据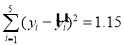 )
)参考公式:相关指数
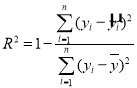
回归方程
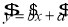 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,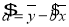 .参考数据:
.参考数据: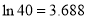 ,
,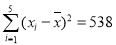 .
.
相关试题

