【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线![]() 和直线
和直线![]() 交于点
交于点![]() .以
.以![]() 为起点,再从曲线
为起点,再从曲线![]() 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为![]() .若
.若![]() 去九寨沟;若
去九寨沟;若![]() 去泰山;若
去泰山;若![]() 去长白山;
去长白山; ![]() 去武夷山.
去武夷山.

(1)若从![]() 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
(2)按上述方案,小明在曲线![]() 上取点
上取点![]() 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点![]() 在曲线
在曲线![]() 上运动,若点
上运动,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)去九寨沟的概率为![]() ,不去泰山的概率为
,不去泰山的概率为![]() ;(2)所以
;(2)所以![]()
【解析】试题分析:
(1) 由题意列出所有可能的事件,结合古典概型公式可得小明去九寨沟的概率为![]() ,不去泰山的概率
,不去泰山的概率![]()
(2)由题意可得![]() ,结合圆的几何意义可得其最大值为
,结合圆的几何意义可得其最大值为![]() .
.
试题解析:
(1)由题意可知得到向量组合方式共有:

共15种
设事件“去九寨沟”=B,“不去泰山”=C
则去九寨沟即ξ>0: ![]()
共4种
![]()
去泰山即=0, ![]()
共4种
![]()
(2)由题意:小明去武夷山即![]()

故可设![]()

![]()
上式几何意义:圆![]() 上的点与点(6,3)的距离
上的点与点(6,3)的距离
上式的最大值即点![]()
距离的最大值,即圆心![]()
的距离再加半径
即![]()
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
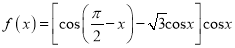
(1)求
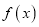 的最小正周期和最大值;
的最小正周期和最大值;(2)讨论
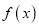 的单调性。
的单调性。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(I)求函数
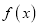 的单调区间;
的单调区间;(Ⅱ)当
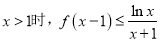 恒成立,求
恒成立,求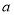 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).
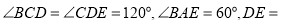
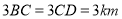 .
.
(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】葫芦岛市某高中进行一项调查:2012年至2016年本校学生人均年求学花销
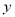 (单位:万元)的数据如下表:
(单位:万元)的数据如下表:年份
2012
2013
2014
2015
2016
年份代号
1
2
3
4
5
年求学花销
3.2
3.5
3.8
4.6
4.9
(1)求
 关于
关于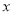 的线性回归方程;
的线性回归方程;(2)利用(1)中的回归方程,分析2012年至2016年本校学生人均年求学花销的变化情况,并预测该地区2017年本校学生人均年求学花销情况.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
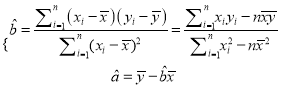
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a∈R,函数
 .
.(I)若函数
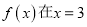 处取得极值,求曲线
处取得极值,求曲线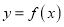 在点
在点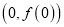 处的切线方程;
处的切线方程;(Ⅱ)若
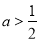 ,函数
,函数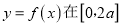 上的最小值是
上的最小值是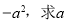 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
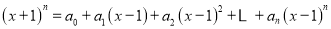 ,(其中
,(其中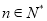 ).
).(1)求
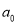 及
及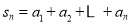 ;
;(2)试比较
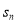 与
与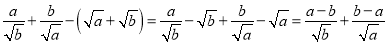 的大小,并用数学归纳法给出证明过程.
的大小,并用数学归纳法给出证明过程.
相关试题

