【题目】已知函数![]()
(1)求![]() 的最小正周期和最大值;
的最小正周期和最大值;
(2)讨论![]() 的单调性。
的单调性。
参考答案:
【答案】(1) 最小正周期为π,最大值为![]()
(2) 在![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
【解析】试题分析:
(1)整理函数的解析式为![]() ,据此可得最小正周期为π,最大值为
,据此可得最小正周期为π,最大值为![]()
(2)利用(1)中函数的解析式可得函数在![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
试题解析:
(1)f(x)=cosxsinx-![]() cos2x
cos2x
=cosxsinx-![]() (1+cos2x)
(1+cos2x)
=![]() sin2x-
sin2x-![]() cos2x-
cos2x-![]()
=sin(2x-![]() )-
)-![]() ,
,
因此f(x)的最小正周期为π,最大值为 1-![]()
(2)由正弦曲线的单调性可知,由-![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2 kπ.可得单调增区间
+2 kπ.可得单调增区间
-![]() +kπ ≤x≤
+kπ ≤x≤ ![]() +kπ
+kπ
由 ![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2 kπ,可得单调减区间
+2 kπ,可得单调减区间
![]() +kπ ≤x≤
+kπ ≤x≤ ![]() +kπ
+kπ
所以f(x)在[-![]() +2kπ,
+2kπ, ![]() +2kπ]上单调递增;在[
+2kπ]上单调递增;在[![]() +kπ,
+kπ, ![]() +kπ]上单调递减.
+kπ]上单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)当
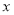 为常数,且
为常数,且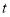 在区间
在区间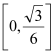 变化时,求
变化时,求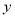 的最小值
的最小值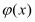 ;
;(2)证明:对任意的
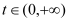 ,总存在
,总存在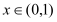 ,使得
,使得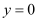 .
. -
科目: 来源: 题型:
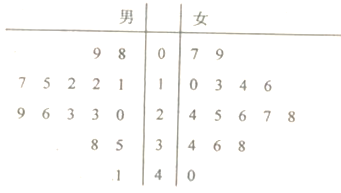
查看答案和解析>>【题目】葫芦岛市某工厂党委为了研究手机对年轻职工工作和生活的影响情况做了一项调查:在厂内用简单随机抽样方法抽取了30名25岁至35岁的职工,对其“每十天累计看手机时间”(单位:小时)进行调查,得到茎叶图如下.所抽取的男职工“每十天累计看手机时间”的平均值和所抽取的女生 “每十天累计看手机时间”的中位数分别是( )
A.
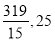 B.
B. 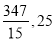 C.
C. 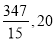 D.
D. 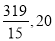
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x﹣
 ﹣(a+2)lnx,其中实数a≥0.
﹣(a+2)lnx,其中实数a≥0.(1)若a=0,求函数f(x)在x∈[1,3]上的最值;
(2)若a>0,讨论函数f(x)的单调性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(I)求函数
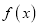 的单调区间;
的单调区间;(Ⅱ)当
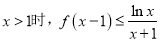 恒成立,求
恒成立,求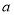 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).
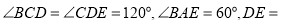
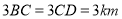 .
.
(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明准备利用暑假时间去旅游,妈妈为小明提供四个景点,九寨沟、泰山、长白山、武夷山.小明决定用所学的数学知识制定一个方案来决定去哪个景点:(如图)曲线
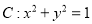 和直线
和直线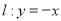 交于点
交于点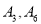 .以
.以 为起点,再从曲线
为起点,再从曲线 上任取两个点分别为终点得到两个向量,记这两个向量的数量积为
上任取两个点分别为终点得到两个向量,记这两个向量的数量积为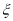 .若
.若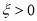 去九寨沟;若
去九寨沟;若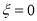 去泰山;若
去泰山;若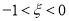 去长白山;
去长白山;  去武夷山.
去武夷山.
(1)若从
 这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;
这六个点中任取两个点分别为终点得到两个向量,分别求小明去九寨沟的概率和不去泰山的概率;(2)按上述方案,小明在曲线
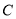 上取点
上取点 作为向量的终点,则小明决定去武夷山.点
作为向量的终点,则小明决定去武夷山.点 在曲线
在曲线 上运动,若点
上运动,若点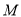 的坐标为
的坐标为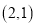 ,求
,求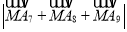 的最大值.
的最大值.
相关试题

