【题目】已知直线![]() 经过点
经过点![]() .
.
(1)若原点到直线![]() 的距离为2,求直线
的距离为2,求直线![]() 的方程;
的方程;
(2)若直线![]() 被两条相交直线
被两条相交直线![]() 和
和![]() 所截得的线段恰被点
所截得的线段恰被点![]() 平分,求直线
平分,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)本题首先可以假设直线![]() 的斜率不存在,然后根据点
的斜率不存在,然后根据点![]() 得出直线方程,再然后假设直线斜率存在并设出直线方程
得出直线方程,再然后假设直线斜率存在并设出直线方程![]() ,最后根据原点到直线
,最后根据原点到直线![]() 的距离为2即可得出结果;
的距离为2即可得出结果;
(2)本题首先可以设出直线![]() 与直线
与直线![]() ,
,![]() 的交点坐标
的交点坐标![]() 、
、![]() 分别为
分别为![]() 、
、![]() ,然后根据中点坐标的相关性质得出
,然后根据中点坐标的相关性质得出![]() 、
、![]() ,再然后根据
,再然后根据![]() 在
在![]() 上以及
上以及![]() 在
在![]() 上得出
上得出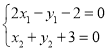 并解得
并解得![]() 的坐标是
的坐标是![]() ,最后根据直线的两点式方程即可得出结果.
,最后根据直线的两点式方程即可得出结果.
(1)①直线![]() 的斜率不存在时,显然成立,直线方程为
的斜率不存在时,显然成立,直线方程为![]() .
.
②当直线斜率存在时,设直线方程为![]() ,
,
由原点到直线![]() 的距离为2得
的距离为2得![]() ,解得
,解得![]() ,
,
故直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
综上,所求直线方程为![]() 或
或![]() .
.
(2)设直线![]() 夹在直线
夹在直线![]() ,
,![]() 之间的线段为
之间的线段为![]() (
(![]() 在
在![]() 上,
上,![]() 在
在![]() 上),
上),
![]() 、
、![]() 的坐标分别设为
的坐标分别设为![]() 、
、![]() ,
,
因为![]() 被点
被点![]() 平分,所以
平分,所以![]() ,
,![]() ,
,
于是![]() ,
,![]()
由于![]() 在
在![]() 上,
上,![]() 在
在![]() 上,即
上,即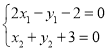 ,解得
,解得![]() ,
,![]() ,
,
即![]() 的坐标是
的坐标是![]() ,故直线
,故直线![]() 的方程是
的方程是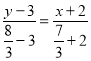 ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆的左焦点为
 ,有一质点A从
,有一质点A从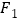 处以速度v开始沿直线运动,经椭圆内壁反射
处以速度v开始沿直线运动,经椭圆内壁反射 无论经过几次反射速率始终保持不变
无论经过几次反射速率始终保持不变 ,若质点第一次回到
,若质点第一次回到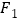 时,它所用的最长时间是最短时间的7倍,则椭圆的离心率e为
时,它所用的最长时间是最短时间的7倍,则椭圆的离心率e为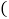
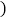
A.
 B.
B. 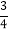 C.
C. 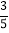 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年的流感来得要比往年更猛烈一些
 据四川电视台
据四川电视台 “新闻现场”播报,近日四川省人民医院一天的最高接诊量超过了一万四千人,成都市妇女儿童中心医院接诊量每天都在九千人次以上
“新闻现场”播报,近日四川省人民医院一天的最高接诊量超过了一万四千人,成都市妇女儿童中心医院接诊量每天都在九千人次以上 这些浩浩荡荡的看病大军中,有不少人都是因为感冒来的医院
这些浩浩荡荡的看病大军中,有不少人都是因为感冒来的医院 某课外兴趣小组趁着寒假假期空闲,欲研究昼夜温差大小与患感冒人数之间的关系,他们分别到成都市气象局与跳伞塔社区医院抄录了去年1到6月每月20日的昼夜温差情况与患感冒就诊的人数,得到如下资料:
某课外兴趣小组趁着寒假假期空闲,欲研究昼夜温差大小与患感冒人数之间的关系,他们分别到成都市气象局与跳伞塔社区医院抄录了去年1到6月每月20日的昼夜温差情况与患感冒就诊的人数,得到如下资料:日期
1月20日
2月20日
3月20日
4月20日
5月20日
6月20日
昼夜温差

10
11
13
12
8
6
就诊人数
 人
人
22
25
29
26
16
12
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
 若选取的是1月与6月的两组数据,请根据2月至5月份的数据,求出y关于x的线性回归方程
若选取的是1月与6月的两组数据,请根据2月至5月份的数据,求出y关于x的线性回归方程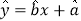 ;
; 若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想? 参考公式:
参考公式: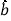
 ,
,

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台为宣传本市,随机对本市内
 岁的人群抽取了
岁的人群抽取了 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.组号
分组
回答正确的人数
回答正确的人数占本组的频率
第1组
[15,25)
a
0.5
第2组
[25,35)
18
x
第3组
[35,45)
b
0.9
第4组
[45,55)
9
0.36
第5组
[55,65]
3
y

(1)分别求出
 的值;
的值;(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆 的圆心在
的圆心在 轴右侧,原点
轴右侧,原点 和点
和点 都在圆
都在圆 上,且圆
上,且圆 在
在 轴上截得的线段长度为3.
轴上截得的线段长度为3.(1)求圆
 的方程;
的方程;(2)若
 ,
, 为圆
为圆 上两点,若四边形
上两点,若四边形 的对角线
的对角线 的方程为
的方程为 ,求四边形
,求四边形 面积的最大值;
面积的最大值;(3)过点
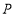 作两条相异直线分别与圆
作两条相异直线分别与圆 相交于
相交于 ,
, 两点,若直线
两点,若直线 ,
, 的斜率分别为
的斜率分别为 ,
, ,且
,且 ,试判断直线
,试判断直线 的斜率是否为定值,并说明理由.
的斜率是否为定值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,抛物线
,抛物线 :
: 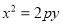 与抛物线
与抛物线 :
:  异于原点
异于原点 的交点为
的交点为 ,且抛物线
,且抛物线 在点
在点 处的切线与
处的切线与 轴交于点
轴交于点 ,抛物线
,抛物线 在点
在点 处的切线与
处的切线与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 .
.(1)若直线
 与抛物线
与抛物线 交于点
交于点 ,
,  ,且
,且 ,求
,求 ;
;(2)证明:
 的面积与四边形
的面积与四边形 的面积之比为定值.
的面积之比为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,且经过点
,且经过点 ,两个焦点分别为
,两个焦点分别为 .
.(1)求椭圆
 的方程;
的方程;(2)过
 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,若
两点,若 的内切圆半径为
的内切圆半径为 ,求以
,求以 为圆心且与直线
为圆心且与直线 相切的圆的方程.
相切的圆的方程.
相关试题

