【题目】如图,江的两岸可近似地看出两条平行的直线,江岸的一侧有![]() ,
, ![]() 两个蔬菜基地,江岸的另一侧点
两个蔬菜基地,江岸的另一侧点![]() 处有一个超市.已知
处有一个超市.已知![]() 、
、![]() 、
、![]() 中任意两点间的距离为
中任意两点间的距离为![]() 千米,超市欲在
千米,超市欲在![]() 之间建一个运输中转站
之间建一个运输中转站![]() ,
, ![]() ,
, ![]() 两处的蔬菜运抵
两处的蔬菜运抵![]() 处后,再统一经过货轮运抵
处后,再统一经过货轮运抵![]() 处,由于
处,由于![]() ,
, ![]() 两处蔬菜的差异,这两处的运输费用也不同.如果从
两处蔬菜的差异,这两处的运输费用也不同.如果从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元.从
元.从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元,货轮的运输费为每千米
元,货轮的运输费为每千米![]() 元.
元.

(1)设![]() ,试将运输总费用
,试将运输总费用![]() (单位:元)表示为
(单位:元)表示为![]() 的函数
的函数![]() ,并写出自变量的取值范围;
,并写出自变量的取值范围;
(2)问中转站![]() 建在何处时,运输总费用
建在何处时,运输总费用![]() 最小?并求出最小值.
最小?并求出最小值.
参考答案:
【答案】(1) ![]() ,
, ![]() ;(2)中转站
;(2)中转站![]() 建在
建在![]() 处
处![]() 千米处时,运输总费用最小的为
千米处时,运输总费用最小的为![]() 元.
元.
【解析】试题分析:
(1)由题意结合正弦定理可得![]() ,
, ![]() .
.
(2)结合(1)的函数解析式求导有![]() ,
, ![]() ,利用导函数研究函数的性质可得中转站
,利用导函数研究函数的性质可得中转站![]() 建在
建在![]() 处
处![]() 千米处时,运输总费用最小的为
千米处时,运输总费用最小的为![]() 元.
元.
试题解析:
(1)在![]() 中,由正弦定理知
中,由正弦定理知
![]() ,则
,则 ,
,
则![]() ,
, ![]() .
.
所以![]() .
.
即![]() ,
, ![]() .
.
(2)![]() ,
, ![]()
令![]() ,
, ![]()
当![]() 时,
时, ![]() ,
, ![]() ;
;
当![]() 时,
时, ![]() ,
, ![]() ,
,
所以当![]() 时,
时, ![]() 取最小值,
取最小值,
此时![]() ,
, ![]() ,
, ![]() .
.
答:中转站![]() 建在
建在![]() 处
处![]() 千米处时,运输总费用最小的为
千米处时,运输总费用最小的为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
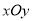 中,以
中,以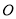 为极点,
为极点, 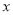 轴的正半轴为极轴建立极坐标系.若直线
轴的正半轴为极轴建立极坐标系.若直线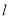 的极坐标方程为
的极坐标方程为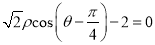 ,曲线
,曲线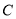 的极坐标方程为
的极坐标方程为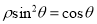 ,将曲线
,将曲线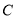 上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线
上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线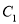 .
.(Ⅰ)求曲线
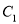 的直角坐标方程;
的直角坐标方程;(Ⅱ)已知直线
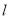 与曲线
与曲线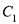 交于
交于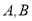 两点,点
两点,点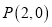 ,求
,求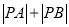 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,函数
,函数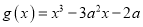 ,(
,( 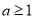 ),若对任意
),若对任意 ,总存在
,总存在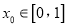 ,使得
,使得 成立,则
成立,则 的取值范围是__________.
的取值范围是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点
的右焦点 ,椭圆
,椭圆 的左,右顶点分别为
的左,右顶点分别为 .过点
.过点 的直线
的直线 与椭圆交于
与椭圆交于 两点,且
两点,且 的面积是
的面积是 的面积的3倍.
的面积的3倍. (Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)若
 与
与 轴垂直,
轴垂直, 是椭圆
是椭圆 上位于直线
上位于直线 两侧的动点,且满足
两侧的动点,且满足 ,试问直线
,试问直线 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x﹣1.
(1)求f(x)的函数解析式;
(2)作出函数f(x)的简图,写出函数f(x)的单调减区间及最值.
(3)若关于x的方程f(x)=m有两个解,试说出实数m的取值范围.(只要写出结果,不用给出证明过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
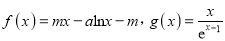 ,其中
,其中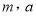 均为实数,
均为实数, 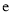 为自然对数的底数.
为自然对数的底数.(I)求函数
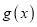 的极值;
的极值;(II)设
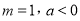 ,若对任意的
,若对任意的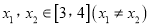 ,
, 恒成立,求实数
恒成立,求实数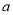 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
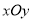 中,曲线
中,曲线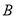 是过点
是过点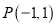 ,倾斜角为
,倾斜角为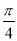 的直线,以直角坐标系
的直线,以直角坐标系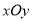 的原点为极点,
的原点为极点, 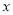 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线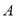 的极坐标方程是
的极坐标方程是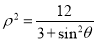 .
.(1)求曲线
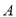 的普通方程和曲线
的普通方程和曲线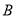 的一个参数方程;
的一个参数方程;(2)曲线
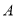 与曲线
与曲线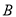 相交于
相交于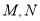 两点,求
两点,求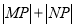 的值.
的值.
相关试题

