【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由20名高二级学生和15名高一级学生组成,现采用分层抽样的方法抽取7人,组成一个体验小组去市场体验“共享单车”的使用.问:
(Ⅰ)应从该兴趣小组中抽取高一级和高二级的学生各多少人;
(Ⅱ)已知该地区有![]() ,
, ![]() 两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租
两种型号的“共享单车”,在市场体验中,该体验小组的高二级学生都租![]() 型车,高一级学生都租
型车,高一级学生都租![]() 型车.
型车.
(1)如果从组内随机抽取3人,求抽取的3人中至少有2人在市场体验过程中租![]() 型车的概率;
型车的概率;
(2)已知该地区![]() 型车每小时的租金为1元,
型车每小时的租金为1元, ![]() 型车每小时的租金为1.2元,设
型车每小时的租金为1.2元,设![]() 为从体验小组内随机抽取3人得到的每小时租金之和,求
为从体验小组内随机抽取3人得到的每小时租金之和,求![]() 的数学期望.
的数学期望.
参考答案:
【答案】(Ⅰ)高一学生人数为3,高二学生的人数为4;(Ⅱ)(1)![]() ,(2)
,(2)![]() .
.
【解析】试题分析:(Ⅰ)利用各年级的比例,抽样即可;
(Ⅱ)(1)从7个人里抽三个,总数为![]() ,计算抽取的3人中至少有2人在市场体验过程中租
,计算抽取的3人中至少有2人在市场体验过程中租![]() 型车的情况,作比即可;
型车的情况,作比即可;
(2)![]() 的可能取值为:3,3.2,3.4,3.6,分别计算概率即可.
的可能取值为:3,3.2,3.4,3.6,分别计算概率即可.
试题解析:
(Ⅰ)依题意知,应从该兴趣小组中抽取的高一学生人数为![]() ,
,
高二学生的人数为: ![]() ;
;
(Ⅱ)(1)解法1:所求的概率![]() .
.
解法2:所求概率![]() .
.
(2)从小组内随机抽取3人, 得到的![]() 的可能取值为:3,3.2,3.4,3.6.(元)
的可能取值为:3,3.2,3.4,3.6.(元)
因![]()
![]()
![]()
![]()
故![]() 的数学期望.
的数学期望. ![]() (元)
(元)
-
科目: 来源: 题型:
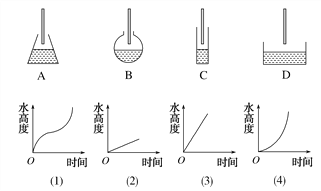
查看答案和解析>>【题目】生活经验告诉我们,当水注进容器(设单位时间内进水量相同)时,水的高度随着时间的变化而变化,在下图中请选择与容器相匹配的图像,A对应________;B对应________;C对应________;D对应________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥
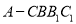 的底面为矩形,D为
的底面为矩形,D为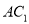 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.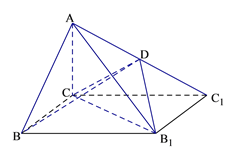
(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=
 ,
,(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
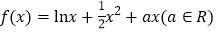 ,
,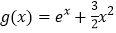 .
.(Ⅰ)讨论
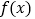 的极值点的个数;
的极值点的个数;(Ⅱ)若对于
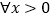 ,总有
,总有 .(i)求实数
.(i)求实数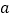 的范围; (ii)求证:对于
的范围; (ii)求证:对于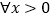 ,不等式
,不等式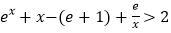 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的
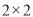 列联表:
列联表:爱好
不爱好
合计
男
20
30
50
女
10
20
30
合计
30
50
80
(Ⅰ)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为
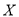 ,求
,求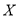 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
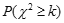
0.050
0.010

3.841
6.635
附:
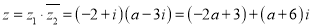
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
R(x)=
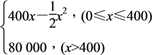
其中x是仪器的月产量.
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少元?(总收益=总成本+利润)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
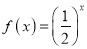 ,函数
,函数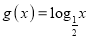 .
.(1)若
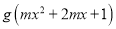 的定义域为
的定义域为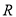 ,求实数
,求实数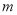 的取值范围;
的取值范围;(2)当
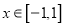 时,求函数
时,求函数 的最小值
的最小值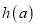 ;
;(3)是否存在非负实数
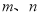 ,使得函数
,使得函数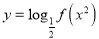 的定义域为
的定义域为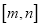 ,值域为
,值域为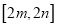 ,若存在,求出
,若存在,求出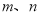 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
相关试题

