搜索
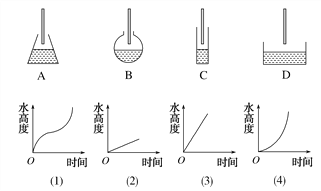
【题目】生活经验告诉我们，当水注进容器(设单位时间内进水量相同)时，水的高度随着时间的变化而变化，在下图中请选择与容器相匹配的图像，A对应________；B对应________；C对应________；D对应________．
参考答案：
【答案】 (4) (1) (2) (3)
【解析】
容器下粗上细，水高度的变化先慢后快，根据导数的几何意义可知，函数图象切线斜率变化故先慢后快， 
与(4)对应； 
容器为球形，水高度变化为快—慢—快，根据导数的几何意义可知， 
应与(1)对应； 
容器都是柱形的，水高度的变化速度都应是直线形，但
容器细， 
容器粗，故水高度的变化为： 
容器快， 
与(3)对应， 
容器慢， 
与(2)对应，故答案为(4) (1) (3) (2)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将圆
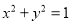上每一点的纵坐标不变，横坐标变为原来的
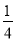，得曲线C.（Ⅰ）写出C的参数方程；
（Ⅱ）设直线l：
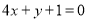与C的交点为P1，P2，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求过线段P1 P2的中点且与l垂直的直线的极坐标方程. -
科目： 来源： 题型：
查看答案和解析>>【题目】某高职院校进行自主招生文化素质考试，考试内容为语文、数学、英语三科，总分为200分.现从上线的考生中随机抽取20人，将其成绩用茎叶图记录如下：
男
女
15
6
5
4
16
3
5
8
8
2
17
2
3
6
8
8
8
6
5
18
5
7
19
2
3
（Ⅰ）计算上线考生中抽取的男生成绩的方差
；（结果精确到小数点后一位）（Ⅱ）从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会，求所选考生恰为一男一女的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD，
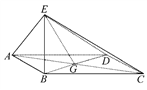
(1)证明：平面AEC⊥平面BED.
(2)若∠ABC=120°，AE⊥EC，三棱锥E-ACD的体积为
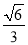，求该三棱锥的侧面积. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四棱锥
的底面为矩形，D为
的中点，AC⊥平面BCC1B1．
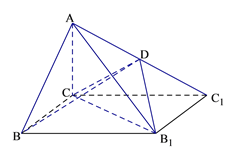
（Ⅰ）证明：AB//平面CDB1;
（Ⅱ）若AC=BC=1，BB1=
,（1）求BD的长；
（2）求B1D与平面ABB1所成角的正弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】函数
，
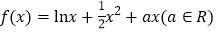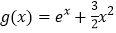．（Ⅰ）讨论
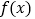的极值点的个数；（Ⅱ）若对于
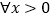，总有
.（i）求实数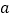
的范围； （ii）求证：对于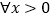，不等式
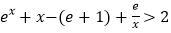成立． -
科目： 来源： 题型：
查看答案和解析>>【题目】某地区以“绿色出行”为宗旨开展“共享单车”业务.该地区某高级中学一兴趣小组由20名高二级学生和15名高一级学生组成，现采用分层抽样的方法抽取7人，组成一个体验小组去市场体验“共享单车”的使用.问：
（Ⅰ）应从该兴趣小组中抽取高一级和高二级的学生各多少人；
（Ⅱ）已知该地区有
, 
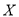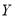两种型号的“共享单车”，在市场体验中，该体验小组的高二级学生都租
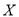型车，高一级学生都租
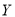型车.（1）如果从组内随机抽取3人，求抽取的3人中至少有2人在市场体验过程中租
型车的概率;（2）已知该地区
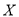型车每小时的租金为1元， 
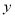型车每小时的租金为1.2元，设
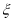为从体验小组内随机抽取3人得到的每小时租金之和，求
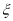的数学期望.
相关试题
