【题目】设![]() .
.
(1)讨论函数![]() 的极值;
的极值;
(2)当![]() 时,
时, ![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)求出函数的导数,通过![]() 与
与![]() 的大小讨论函数的单调性,进而可得到函数的极值;(2)设
的大小讨论函数的单调性,进而可得到函数的极值;(2)设![]() ,则
,则![]() ,通过
,通过![]() 时,通过函数的单调性,函数的最值,求解
时,通过函数的单调性,函数的最值,求解![]() 的取值范围.
的取值范围.
试题解析:(1)![]() ,
,
若![]() ,则
,则![]() ,
, ![]() 在
在![]() 上单调递增,没有极值.
上单调递增,没有极值.
若![]() ,令
,令![]() ,
, ![]() ,列表
,列表
|
|
|
|
|
|
|
|
|
|
|
|
所以当![]() 时,
时, ![]() 有极小值
有极小值![]() ,没有极大值.
,没有极大值.
(2)方法1
设![]() ,则
,则![]() .
.
从而当![]() ,即
,即![]() 时,
时, ![]()
![]() ,
, ![]() ,
, ![]() 在
在![]() 单调递增,于是当
单调递增,于是当![]() 时,
时, ![]() .
.
当![]() 时,若
时,若![]() ,则
,则![]() ,
, ![]() ,
, ![]() 在
在![]() 单调递减,于是当
单调递减,于是当![]() 时,
时, ![]() .
.
综合得![]() 的取值范围为
的取值范围为![]() .
.
(2)方法2
由(1)当![]() 时,
时, ![]() ,得
,得![]() .
.
(2)设![]() ,则
,则![]()
![]() .从而当
.从而当![]() ,即
,即![]() 时,
时, ![]()
![]() ,而
,而![]() ,于是当
,于是当![]() 时,
时, ![]() .
.
由![]()
![]() 可得,
可得, ![]() ,即
,即![]()
![]() ,从而当
,从而当![]() 时,
时, ![]() .故当
.故当![]() 时,
时, ![]() ,而
,而![]() ,于是当
,于是当![]() 时,
时, ![]() .
.
综合得![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一建筑物的三视图(单位:
 ),现需将其外壁用油漆粉刷一遍,已知每平方米用漆
),现需将其外壁用油漆粉刷一遍,已知每平方米用漆 ,问需要油漆多少千克?(无需求近似值)
,问需要油漆多少千克?(无需求近似值)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2-bx+3.
(1)若f(0)=f(4),求函数f(x)的零点;
(2)若函数f(x)一个零点大于1,另一个零点小于1,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家医药研究所,从中草药中提取并合成了甲、乙两种抗“
 病毒”的药物,经试验,服用甲、乙两种药物痊愈的概率分别为
病毒”的药物,经试验,服用甲、乙两种药物痊愈的概率分别为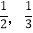 .现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”.
.现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”.(1)求一个试用组为“甲类组”的概率;
(2)观察3个试用组,用
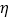 表示这3个试用组中“甲类组”的个数,求
表示这3个试用组中“甲类组”的个数,求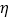 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=x2-2x-3,求f(3),f(-5),f(5),并计算f(3)+f(-5)+f(5)的值.设计出解决该问题的一个算法,并画出程框图.
-
科目: 来源: 题型:
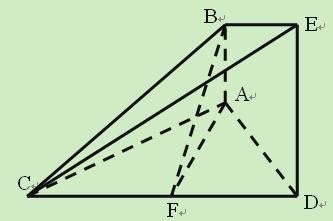
查看答案和解析>>【题目】(本小题满分14分)
如图的几何体中,
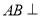 平面
平面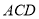 ,
, 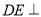 平面
平面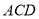 ,△
,△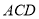 为等边三角形
为等边三角形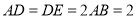 ,
, 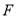 为
为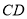 的中点.
的中点.(1)求证:
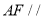 平面
平面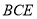 ;
;(2)求证:平面
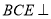 平面
平面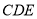 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25) , [25,30) , [30,35), [35,40) , [40,45] ,并得到如下频率分布直方图.
(Ⅰ)求图中
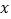 的值,并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数;
的值,并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数;(Ⅱ)在抽取的100名志愿者中按年龄分层抽取10名参加区电视台“文明伴你行”节目录制,再从这10名志愿者中随机选取3名到现场分享劝导制止行人闯红灯的经历,记这3名志愿者中年龄不低于35岁的人数为
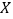 ,求
,求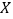 的分布列及数学期望.
的分布列及数学期望.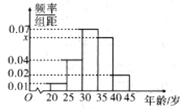
相关试题

