【题目】已知数列{an}的前n项和Sn=﹣an﹣( ![]() )n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
)n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
(Ⅰ)求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)设cn=log2 ![]() ,数列{
,数列{ ![]() }的前n项和为Tn , 求满足Tn
}的前n项和为Tn , 求满足Tn ![]() (n∈N*)的n的最大值.
(n∈N*)的n的最大值.
参考答案:
【答案】(Ⅰ)证明:∵Sn=﹣an﹣( ![]() )n﹣1+2(n∈N+),当n≥2时,Sn﹣1=﹣an﹣1﹣(
)n﹣1+2(n∈N+),当n≥2时,Sn﹣1=﹣an﹣1﹣( ![]() )n﹣2+2(n∈N+),
)n﹣2+2(n∈N+),
∴an=Sn﹣Sn﹣1=﹣an+an﹣1+( ![]() )n﹣1 ,
)n﹣1 ,
化为2nan=2n﹣1an﹣1+1.
∵bn=2nan . ∴bn=bn﹣1+1,即当n≥2时,bn﹣bn﹣1=1.
令n=1,可得S1=﹣a1﹣1+2=a1 , 即a1= ![]() .
.
又b1=2a1=1,∴数列{bn}是首项和公差均为1的等差数列.
于是bn=1+(n﹣1)1=n=2nan ,
∴an= ![]() .
.
(Ⅱ)解:∵cn=log2![]() =n,
=n,
∴ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴Tn=(1﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…(
)+…( ![]() ﹣
﹣ ![]() )=1+
)=1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ,
,
由Tn![]() ,得1+
,得1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ,即
,即 ![]() +
+ ![]() >
> ![]() ,
,
∵f(n)= ![]() +
+ ![]() 单调递减,f(4)=
单调递减,f(4)= ![]() ,f(5)=
,f(5)= ![]() ,
,
∴n的最大值为4.
【解析】(Ⅰ)利用“当n≥2时,an=Sn﹣Sn﹣1”及其等差数列的通项公式即可得出.(Ⅱ)先求通项,再利用裂项法求和,进而解不等式,即可求得正整数n的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=sin(
 x﹣
x﹣  )﹣2cos2
)﹣2cos2  x+1.
x+1.
(1)求f(x)的最小正周期;
(2)若函数y=f(x)与y=g(x)的图象关于直线x=1对称,求当x∈[0, ]时,y=g(x)的最大值.
]时,y=g(x)的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 
(1)求证AM∥平面BDE;
(2)求二面角A﹣DF﹣B的大小;
(3)试在线段AC上一点P,使得PF与CD所成的角是60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸末,甲申、乙酉、丙戌…癸巳,…,共得到
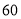 个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()A. 己亥年 B. 戊戌年 C. 庚子年 D. 辛丑年
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆C:
 =1(a>b>0)的中心在原点,焦点在x轴上,焦距为2,且与椭圆x2+
=1(a>b>0)的中心在原点,焦点在x轴上,焦距为2,且与椭圆x2+  =1有相同离心率,直线l:y=kx+m与椭圆C交于不同的A,B两点.
=1有相同离心率,直线l:y=kx+m与椭圆C交于不同的A,B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足 ,(O为坐标原点),求实数λ取值范围.
,(O为坐标原点),求实数λ取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.
(Ⅰ)若a=﹣1,证明:函数f(x)是(0,+∞)上的减函数;
(Ⅱ)若曲线y=f(x)在点(1,f(1))处的切线与直线x﹣y=0平行,求a的值;
(Ⅲ)若x>0,证明: (其中e=2.71828…是自然对数的底数).
(其中e=2.71828…是自然对数的底数).
相关试题

