【题目】在平面直角坐标系中,点![]() ,点
,点![]() .已知抛物线
.已知抛物线![]() (
(![]() 是常数),顶点为
是常数),顶点为![]() .
.
(1)当抛物线经过点![]() 时,求顶点
时,求顶点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴下方,当
轴下方,当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(3)无论![]() 取何值,该抛物线都经过定点
取何值,该抛物线都经过定点![]() .当
.当![]() 时,求抛物线的解析式.
时,求抛物线的解析式.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)将点![]() 坐标代入解析式求得
坐标代入解析式求得![]() 的值即可得;
的值即可得;
(2)先求出顶点![]() 的坐标
的坐标 ,根据
,根据![]() 知点
知点![]() 在第四象限且
在第四象限且![]() ,列出关于
,列出关于![]() 的方程,解知可得;
的方程,解知可得;
(3)由![]() 知
知![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,分别过点
,分别过点![]() ,
,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,证
,证![]() 得
得![]() ,据此知点
,据此知点![]() 的坐标为
的坐标为![]() 或
或![]() ,再求出直线
,再求出直线![]() 的解析式,将点
的解析式,将点![]() 的坐标代入求得
的坐标代入求得![]() 的值即可得出答案.
的值即可得出答案.
(1)![]() 抛物线
抛物线![]() 经过点
经过点![]()
![]()
解得:![]()
![]() 抛物线解析式为
抛物线解析式为![]()
![]()
![]() 顶点
顶点![]() 的坐标为
的坐标为![]() ;
;
(2)抛物线![]() 的顶点
的顶点![]() 的坐标为
的坐标为 ,
,
由点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的下方,
轴的下方,![]() 知点
知点![]() 在第四象限,如图1,过点
在第四象限,如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,

则![]() ,可知
,可知![]() ,即
,即![]() ,
,
解得:![]()
当![]() 时,点
时,点![]() 不在第四象限,舍去;
不在第四象限,舍去;
![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
(3)由![]() ,可知当
,可知当![]() 时,无论
时,无论![]() 取何值时
取何值时![]() 都等于
都等于![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,分别过点
,分别过点![]() ,
,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]()

则![]()
![]()
![]()
![]()
![]()
![]()
![]()
则点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
①当点![]() 的坐标为
的坐标为![]() 时,可得直线
时,可得直线![]() 的解析式为
的解析式为![]()
![]() 点
点 在直线
在直线![]() 上,
上,
![]() ,
,
当![]() 时,点
时,点![]() 与点
与点![]() 重合,不符合题意,
重合,不符合题意,
![]() ;
;
②当点![]() 的坐标为
的坐标为![]() 时,可得直线
时,可得直线![]() 的解析式为
的解析式为![]() ,
,
![]() 点
点 在直线
在直线![]() 上,
上,
![]() ,
,
解得:![]() 或
或![]() ,
,
则抛物线的解析式为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是南北方向的一条公路,
是南北方向的一条公路, 是北偏东
是北偏东 方向的一条公路,某风景区的一段边界为曲线
方向的一条公路,某风景区的一段边界为曲线 .为方便游客光,拟过曲线
.为方便游客光,拟过曲线 上的某点分别修建与公路
上的某点分别修建与公路 ,
, 垂直的两条道路
垂直的两条道路 ,
, ,且
,且 ,
, 的造价分别为5万元
的造价分别为5万元 百米,40万元
百米,40万元 百米,建立如图所示的直角坐标系
百米,建立如图所示的直角坐标系 ,则曲线符合函数
,则曲线符合函数 模型,设
模型,设 ,修建两条道路
,修建两条道路 ,
, 的总造价为
的总造价为 万元,题中所涉及的长度单位均为百米.
万元,题中所涉及的长度单位均为百米.(1)求
 解析式;
解析式;(2)当
 为多少时,总造价
为多少时,总造价 最低?并求出最低造价.
最低?并求出最低造价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
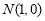 、
、 ,点
,点 是圆
是圆 上一动点,线段
上一动点,线段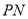 的垂直平分线交线段
的垂直平分线交线段 于点
于点 ,设点
,设点 的轨迹为曲线
的轨迹为曲线 .且直线
.且直线 交曲线
交曲线 于
于 两点(点
两点(点 在
在 轴的上方).
轴的上方).
(1)求曲线
 的方程;
的方程;(2)试判断直线
 与曲线
与曲线 的另一交点
的另一交点 是否与点
是否与点 关于
关于 轴对称?
轴对称? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,四边形
 是矩形,点
是矩形,点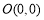 ,点
,点 ,点
,点 .以点
.以点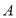 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形 ,得到矩形
,得到矩形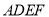 ,点
,点 的对应点分别为
的对应点分别为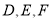 .
.
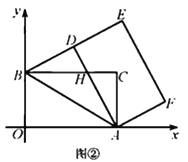
(1)如图①,当点
 落在
落在 边上时,求点
边上时,求点 的坐标;
的坐标;(2)如图②,当点
 落在线段
落在线段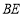 上时,
上时, 与
与 交于点
交于点 .
.①求证
 ;②求点
;②求点 的坐标.
的坐标.(3)记
 为矩形
为矩形 对角线的交点,
对角线的交点, 为
为 的面积,求
的面积,求 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上函数
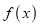 ,若函数
,若函数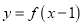 关于点
关于点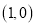 对称,且
对称,且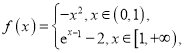 则关于x的方程
则关于x的方程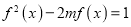 (
(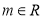 )有n个不同的实数解,则n的所有可能的值为( )
)有n个不同的实数解,则n的所有可能的值为( )A.2B.4
C.2或4D.2或4或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 上一点
上一点 与两焦点构成的三角形的周长为6,离心率为
与两焦点构成的三角形的周长为6,离心率为 ,
, 
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)过点
 的直线
的直线 交椭圆
交椭圆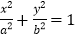 于
于 两点,问在
两点,问在 轴上是否存在定点
轴上是否存在定点 ,使得
,使得 为定值?证明你的结论.
为定值?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4
 4:坐标系与参数方程:在直角坐标系xoy中,曲线
4:坐标系与参数方程:在直角坐标系xoy中,曲线 的参数方程为
的参数方程为 ,(
,( 为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线
为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)设P为曲线C1上的动点,求点P到C2上点的距离的最小值.
相关试题

