【题目】下列命题正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“x=5”是“x2﹣4x﹣5=0”的充分不必要条件
C.命题“若x<﹣1,则x2﹣2x﹣3>0”的否定为:“若x≥﹣1,则x2﹣2x﹣3≤0”
D.已知命题 p:x∈R,x2+x﹣1<0,则p:x∈R,x2+x﹣1≥0
参考答案:
【答案】B
【解析】解:选项A,若p∨q为真命题,则p与q有一个为真,但p∧q为不一定为真命题,故不正确;
选项B,“x=5”能得到“x2﹣4x﹣5=0”,“x2﹣4x﹣5=0”不能推出“x=5”,则“x=5”是“x2﹣4x﹣5=0”的充分不必要条件,故正确;
选项C,命题“若x<﹣1,则x2﹣2x﹣3>0”的否定为:“若x<﹣1,则x2﹣2x﹣3≤0”,故不正确;
选项D,已知命题 p:x∈R,x2+x﹣1<0,则p:x∈R,x2+x﹣1≥0,故不正确.
所以答案是:B.
【考点精析】根据题目的已知条件,利用特称命题和命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握特称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;特称命题的否定是全称命题;两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.
;特称命题的否定是全称命题;两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人参加普法知识竞赛,共有5个不同题目,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)求甲抽到判断题,乙抽到选择题的概率是多少;
(2)求甲、乙两人中至少有一人抽到选择题的概率是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图所示的程序框图

(1)当输入的x为2,﹣1时,分别计算输出的y值,并写出输出值y关于输入值x的函数关系式;
(2)当输出的结果为4时,求输入的x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求求值:
(1)用辗转相除法求123和48的最大公约数.
(2)用更相减损术求80和36的最大公约数.
(3)把89化为二进制数. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两船驶向一个不能同时停泊两艘船的码头,它们在一天二十四小时内到达该码头的时刻是等可能的.如果甲船停泊时间为1小时,乙船停泊时间为2小时,求它们中的任意一艘都不需要等待码头空出的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生.
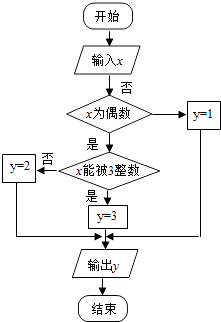
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)运行
次数n输出y的值
为1的频数输出y的值
为2的频数输出y的值
为3的频数30
14
6
10
…
…
…
…
2100
1027
376
697
乙的频数统计表(部分)
运行
次数n输出y的值
为1的频数输出y的值
为2的频数输出y的值
为3的频数30
12
11
7
…
…
…
…
2100
1051
696
353
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数据
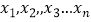 是上海普通职工n
是上海普通职工n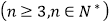 个人的年收入,设n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入
个人的年收入,设n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入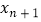 , 则这n+1个数据中,下列说法正确的是 ( )
, 则这n+1个数据中,下列说法正确的是 ( )
A.年收入平均数大大增加,中位数一定变大,方差可能不变
B.年收入平均数大大增加,中位数可能不变,方差变大
C.年收入平均数大大增加,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
相关试题

