【题目】已知函数f(x)=log2 ![]() . (Ⅰ)判断f(x)奇偶性并证明;
. (Ⅰ)判断f(x)奇偶性并证明;
(Ⅱ)用单调性定义证明函数g(x)= ![]() 在函数f(x)定义域内单调递增,并判断f(x)=log2
在函数f(x)定义域内单调递增,并判断f(x)=log2 ![]() 在定义域内的单调性.
在定义域内的单调性.
参考答案:
【答案】解:(Ⅰ)由 ![]() >0,求得﹣1<x<1,故函数f(x)的定义域为(﹣1,1), 再根据f(﹣x)=
>0,求得﹣1<x<1,故函数f(x)的定义域为(﹣1,1), 再根据f(﹣x)= ![]() =﹣log2
=﹣log2![]() =﹣f(x),故函数f(x)为奇函数.
=﹣f(x),故函数f(x)为奇函数.
(Ⅱ)设﹣1<x1<x2<1,∵g(x1)﹣g(x2)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∵﹣1<x1<x2<1,∴x1﹣x2<0,1﹣x1>0,1﹣x2>0,∴g(x1)<g(x2),
∴g(x)= ![]() 在(﹣1,1)内为增函数.
在(﹣1,1)内为增函数.
令g(x)=t,则f(x)=log2t,故f(x)在定义域内的单调性与t的单调性相同,
由于t在定义域(﹣1,1)内但地递增,故f(x)在定义域(﹣1,1)内的单调递增
【解析】(Ⅰ)由 ![]() >0,求得函数f(x)的定义域为(﹣1,1),关于原点对称,再根据f(﹣x)=﹣f(x),可得函数f(x)为奇函数.(Ⅱ)设﹣1<x1<x2<1,求得 g(x1)﹣g(x2)<0,可得g(x)在(﹣1,1)内为增函数.令g(x)=t,则f(x)=log2t,故本题即求函数t在(﹣1,1)内的单调性相同,由此得出结论.
>0,求得函数f(x)的定义域为(﹣1,1),关于原点对称,再根据f(﹣x)=﹣f(x),可得函数f(x)为奇函数.(Ⅱ)设﹣1<x1<x2<1,求得 g(x1)﹣g(x2)<0,可得g(x)在(﹣1,1)内为增函数.令g(x)=t,则f(x)=log2t,故本题即求函数t在(﹣1,1)内的单调性相同,由此得出结论.
【考点精析】根据题目的已知条件,利用奇偶性与单调性的综合的相关知识可以得到问题的答案,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
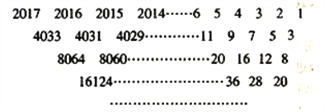
A.
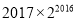 B.
B. 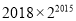 C.
C. 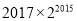 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线
 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的 ,得到曲线
,得到曲线 ,以坐标原点
,以坐标原点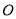 为极点,
为极点, 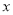 轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系,  的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求曲线
 的参数方程;
的参数方程;(Ⅱ)过原点
 且关于
且关于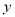 轴对称的两条直线
轴对称的两条直线 与
与 分别交曲线
分别交曲线 于
于 、
、 和
和 、
、 ,且点
,且点 在第一象限,当四边形
在第一象限,当四边形 的周长最大时,求直线
的周长最大时,求直线 的普通方程.
的普通方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 = x·ex,
= x·ex, 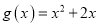 ,
,  ,若对任意的
,若对任意的 ,都有
,都有 成立,则实数k的取值范围是
成立,则实数k的取值范围是A.
 B.
B.  C.
C. 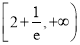 D.
D. 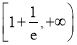
-
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)函数f(x)满足对任意的实数x,y都有f(xy)=f(x)+f(y),且f(4)=2,求f(
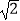 )的值; (Ⅱ)已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(x)在[﹣1,1]上递增,求不等式f(x+
)的值; (Ⅱ)已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(x)在[﹣1,1]上递增,求不等式f(x+  )+f(x﹣1)<0
)+f(x﹣1)<0
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产的新产品必须先靠广告打开销路,该产品广告效应y(单位:元)是产品的销售额与广告费x(单位:元)之间的差,如果销售额与广告费x的算术平方根成正比,根据对市场的抽样调查,每付出100元的广告费,所得销售额是1000元. (Ⅰ)求出广告效应y与广告费x之间的函数关系式;
(Ⅱ)该企业投入多少广告费才能获得最大的广告效应?是不是广告费投入越多越好? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ﹣
﹣ 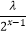 +3(﹣1≤x≤2).
+3(﹣1≤x≤2).
(1)若λ= 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)若函数f(x)的最小值是1,求实数λ的值.
相关试题

