【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线![]() 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的参数方程;
的参数方程;
(Ⅱ)过原点![]() 且关于
且关于![]() 轴对称的两条直线
轴对称的两条直线![]() 与
与![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且点
,且点![]() 在第一象限,当四边形
在第一象限,当四边形![]() 的周长最大时,求直线
的周长最大时,求直线![]() 的普通方程.
的普通方程.
参考答案:
【答案】(1) ![]() (
(![]() 为参数).(2)
为参数).(2)![]()
【解析】试题分析:(Ⅰ)首先求得![]() 的普通方程,由此可求得
的普通方程,由此可求得![]() 的参数方程;(Ⅱ)设四边形
的参数方程;(Ⅱ)设四边形![]() 的周长为
的周长为![]() ,点
,点![]() ,然后得到
,然后得到![]() 与
与![]() 的关系式,从而利用辅助角公式求得点的直角坐标点,从而求得
的关系式,从而利用辅助角公式求得点的直角坐标点,从而求得![]() 的普通方程.
的普通方程.
试题解析:(Ⅰ) ![]() ,
, ![]() (
(![]() 为参数).
为参数).
(Ⅱ)设四边形![]() 的周长为
的周长为![]() ,设点
,设点![]() ,
,
![]()
![]() ,
,
且![]() ,
, ![]() ,
,
所以,当![]() (
(![]() )时,
)时, ![]() 取最大值,
取最大值,
此时![]() ,
,
所以, ![]() ,
, ![]() ,
,
此时, ![]() ,
, ![]() 的普通方程为
的普通方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第十二届全国人名代表大会第五次会议和政协第十二届全国委员会第五次会议(简称两会)分别于2017年3月5日和3月3日在北京开幕,某高校学生会为了解该校学生对全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类,已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为
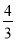 ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.(1)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人参与两会宣传活动,求这2人全是男生的概率.
(2)根据题意建立
 列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?
列联表,并判断是否有99%的把握认为男生与女生对两会的关注有差异?附:
 ,其中
,其中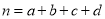 .
.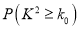
0.100
0.050
0.010
0.001
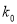
2.706
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
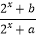 ,是定义在R上的奇函数. (Ⅰ)求函数f(x)的解析式;
,是定义在R上的奇函数. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】“杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( )
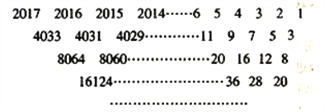
A.
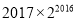 B.
B. 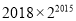 C.
C. 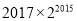 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 = x·ex,
= x·ex, 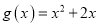 ,
,  ,若对任意的
,若对任意的 ,都有
,都有 成立,则实数k的取值范围是
成立,则实数k的取值范围是A.
 B.
B.  C.
C. 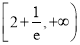 D.
D. 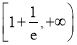
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log2
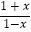 . (Ⅰ)判断f(x)奇偶性并证明;
. (Ⅰ)判断f(x)奇偶性并证明;
(Ⅱ)用单调性定义证明函数g(x)=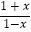 在函数f(x)定义域内单调递增,并判断f(x)=log2
在函数f(x)定义域内单调递增,并判断f(x)=log2 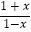 在定义域内的单调性.
在定义域内的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)函数f(x)满足对任意的实数x,y都有f(xy)=f(x)+f(y),且f(4)=2,求f(
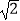 )的值; (Ⅱ)已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(x)在[﹣1,1]上递增,求不等式f(x+
)的值; (Ⅱ)已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(x)在[﹣1,1]上递增,求不等式f(x+  )+f(x﹣1)<0
)+f(x﹣1)<0
的解集.
相关试题

