【题目】
在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6位选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如下图所示的茎叶图.为了增加结果的神秘感,主持人暂时没有公布甲、乙两班最后一位选手的成绩.
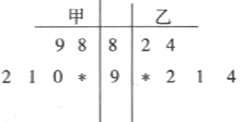
(Ⅰ)求乙班总分超过甲班的概率;
(Ⅱ)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.请你从平均分和方差的角度来分析两个班的选手的情况.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)甲班选手间的实力相当,相差不大,乙班选手间实力悬殊,差距较大.
;(Ⅱ)甲班选手间的实力相当,相差不大,乙班选手间实力悬殊,差距较大.
【解析】试题分析:(Ⅰ)先分别求出甲班前5位选手的总分和乙班前5位选手的总分,由此利用列举法能求出乙班总分超过甲班的概率;(Ⅱ)分别求出甲、乙两班的平均分、方差,由此能求出结果.
试题解析:(Ⅰ)甲班前5位选手的总分为![]() ,
,
乙班前5位选手的总分为![]() ,
,
若乙班总分超过甲班,则甲、乙两班第六位选手的成绩可分别为![]() ,
,![]() ,
,![]() 三种.
三种.
所以,乙班总分超过甲班的概率为![]() .
.
(Ⅱ)甲班平均分为![]() ,
,
乙班平均分为![]() ,
,
![]() ,
,![]() .
.
两班的平均分相同,但甲班选手的方差小于乙班,所以甲班选手间的实力相当,相差不大,乙班选手间实力悬殊,差距较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
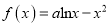 .
.(1)当
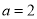 时,求函数
时,求函数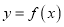 在
在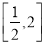 上的最大值;
上的最大值;(2)令
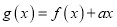 ,若
,若 在区间
在区间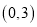 上为单调递增函数,求
上为单调递增函数,求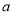 的取值范围;
的取值范围;(3)当
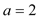 时,函数
时,函数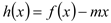 的图象与
的图象与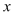 轴交于两点
轴交于两点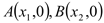 ,且
,且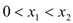 ,又
,又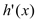 是
是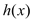 的导函数.若正常数
的导函数.若正常数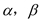 满足条件
满足条件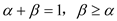 .试比较
.试比较 与0的关系,并给出理由.
与0的关系,并给出理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作
不积极参加班级工作
合计
学习积极性高
18
7
25
学习积极性不高
6
19
25
合计
24
26
50
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:
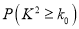
0.10
0.05
0.025
0.010
0.005
0.001
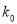
2.706
3.841
5.024
6.635
7.879
10.828
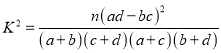
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为
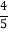 ,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.附表及公式:
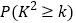
0.15
0.10
0.05
0.025
0.010
0.005
0.001
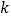
2.072
2.706
3.841
5.024
6.635
7.879
10.828
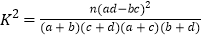
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
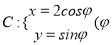 为参数),
为参数), 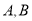 是
是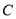 上的动点,且满足
上的动点,且满足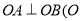 为坐标原点),以原点
为坐标原点),以原点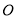 为极点,
为极点, 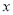 轴的正半轴为极轴建立坐标系,点
轴的正半轴为极轴建立坐标系,点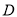 的极坐标为
的极坐标为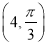 .
.(1)求线段
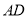 的中点
的中点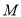 的轨迹
的轨迹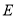 的普通方程;
的普通方程;(2)利用椭圆
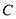 的极坐标方程证明
的极坐标方程证明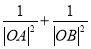 为定值,并求面积的最大值.
为定值,并求面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用
过度使用
合计
未患颈椎病
15
5
20
患颈椎病
10
20
30
合计
25
25
50
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为
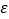 ,求
,求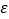 的分布列及数学期望.
的分布列及数学期望.参考数据与公式:
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828

相关试题

