搜索
【题目】已知a，b，c分别为△ABC三个内角A，B，C的对边，c= 
asinC﹣ccosA．
（1）求A；
（2）若a=2，△ABC的面积为 ，求b，c．
参考答案：
【答案】
（1）解：c= 
asinC﹣ccosA，由正弦定理有：
sinAsinC﹣sinCcosA﹣sinC=0，即sinC（ sinA﹣cosA﹣1）=0，
又，sinC≠0，
所以 sinA﹣cosA﹣1=0，即2sin（A﹣ 
）=1，
所以A= 
（2）解：S△ABC= 
bcsinA= ，所以bc=4，
a=2，由余弦定理得：a2=b2+c2﹣2bccosA，即4=b2+c2﹣bc，
即有 
，
解得b=c=2
【解析】（1）由正弦定理有： sinAsinC﹣sinCcosA﹣sinC=0，可以求出A；（2）有三角形面积以及余弦定理，可以求出b、c．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆C的圆心在直线x﹣2y=0上．
（1）若圆C与y轴的正半轴相切，且该圆截x轴所得弦的长为2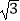
，求圆C的标准方程；
（2）在（1）的条件下，直线l：y=﹣2x+b与圆C交于两点A，B，若以AB为直径的圆过坐标原点O，求实数b的值；
（3）已知点N（0，3），圆C的半径为3，且圆心C在第一象限，若圆C上存在点M，使MN=2MO（O为坐标原点），求圆心C的纵坐标的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】设f（x）=x2+bx+c且f（0）=f（2），则（ ）
A.f（﹣2）＜f（0）＜f（
）
B.f（ ）＜f（0）＜f（﹣2）??
C.f（ ）＜f（﹣2）＜f（0）
D.f（0）＜f（ ）＜f（﹣2） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知顶点在单位圆上的△ABC中，角A、B、C所对的边分别为a、b、c，且b2+c2=a2+bc．
（1）求角A的大小；
（2）若b2+c2=4，求△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】若直角坐标平面内的两点P、Q满足条件：
①P、Q都在函数y=f（x）的图象上；
②P、Q关于原点对称，则称点对[P，Q]是函数y=f（x）的一对“友好点对”（点对[P，Q]与[Q，P]看作同一对“友好点对”），
已知函数f（x）=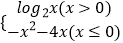
，则此函数的“友好点对”有（ ）
A.0对
B.1对
C.2对
D.3对 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数y=
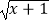+lg（2﹣x）的定义域是集合M，集合N={x|x（x﹣3）＜0}
（1）求M∪N；
（2）求（RM）∩N． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
在
和
处取得极值.（1）求f（x）的表达式和极值．
（2）若f（x）在区间[m，m+4]上是单调函数，试求m的取值范围．
相关试题
