搜索
【题目】设f（x）=x2+bx+c且f（0）=f（2），则（ ）
A.f（﹣2）＜f（0）＜f（ 
）
B.f（ ）＜f（0）＜f（﹣2）??
C.f（ ）＜f（﹣2）＜f（0）
D.f（0）＜f（ ）＜f（﹣2）
参考答案：
【答案】B
【解析】解：∵f（0）=f（2），
∴f（x）的对称轴为x=1，∴f（ 
）=f（ 
）．
∵f（x）的图象开口向上，
∴f（x）在（﹣∞，1）上单调递减，
∵﹣2＜0＜ ，
∴f（﹣2）＞f（0）＞f（ ）=f（ ），
故选B．
【考点精析】根据题目的已知条件，利用二次函数的性质的相关知识可以得到问题的答案，需要掌握当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=Asin（ωx+θ）（ A＞0，ω＞0，|θ|＜
）的最小正周期为π，且图象上有一个最低点为M（ 
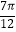，﹣3）．
（1）求f（x）的解析式；
（2）求函数f（x）在[0，π]的单调递增区间． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）对一切x，y∈R都有f（x+y）﹣f（y）=x（x+2y+1）成立，且f（1）=0．
（1）求f（0）的值；
（2）求f（x）的解析式；
（3）已知a∈R，设P：当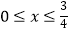
时，不等式f（x）+3＜2x+a恒成立，Q：当x∈[﹣2，2]时，g（x）=f（x）﹣ax是单调函数，如果记使P成立的实数a的取值的集合为A，使Q成立的实数a的取值的集合为B，求A∩RB． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆C的圆心在直线x﹣2y=0上．
（1）若圆C与y轴的正半轴相切，且该圆截x轴所得弦的长为2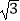
，求圆C的标准方程；
（2）在（1）的条件下，直线l：y=﹣2x+b与圆C交于两点A，B，若以AB为直径的圆过坐标原点O，求实数b的值；
（3）已知点N（0，3），圆C的半径为3，且圆心C在第一象限，若圆C上存在点M，使MN=2MO（O为坐标原点），求圆心C的纵坐标的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知顶点在单位圆上的△ABC中，角A、B、C所对的边分别为a、b、c，且b2+c2=a2+bc．
（1）求角A的大小；
（2）若b2+c2=4，求△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b，c分别为△ABC三个内角A，B，C的对边，c=
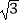asinC﹣ccosA．
（1）求A；
（2）若a=2，△ABC的面积为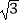 ，求b，c． -
科目： 来源： 题型：
查看答案和解析>>【题目】若直角坐标平面内的两点P、Q满足条件：
①P、Q都在函数y=f（x）的图象上；
②P、Q关于原点对称，则称点对[P，Q]是函数y=f（x）的一对“友好点对”（点对[P，Q]与[Q，P]看作同一对“友好点对”），
已知函数f（x）=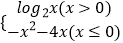
，则此函数的“友好点对”有（ ）
A.0对
B.1对
C.2对
D.3对
相关试题
