【题目】已知函数![]() (
(![]() 且
且![]() 为常数).
为常数).
(1)当![]() 时,讨论函数
时,讨论函数![]() 在
在![]() 的单调性;
的单调性;
(2)设![]() 可求导数,且它的导函数
可求导数,且它的导函数![]() 仍可求导数,则
仍可求导数,则![]() 再次求导所得函数称为原函数
再次求导所得函数称为原函数![]() 的二阶函数,记为
的二阶函数,记为![]() ,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间
,利用二阶导函数可以判断一个函数的凹凸性.一个二阶可导的函数在区间![]() 上是凸函数的充要条件是这个函数在
上是凸函数的充要条件是这个函数在![]() 的二阶导函数非负.
的二阶导函数非负.
若![]() 在
在![]() 不是凸函数,求
不是凸函数,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)将![]() 代入函数
代入函数![]() 的解析式,利用导函数与原函数的关系讨论函数的单调性即可;
的解析式,利用导函数与原函数的关系讨论函数的单调性即可;
(2)利用题中所给的新知识结合题意考查函数的二次导函数,将问题转化为恒成立问题,据此求解实数![]() 的取值范围即可.
的取值范围即可.
试题解析:
(I) ![]() 令
令![]() 得
得![]()
设![]() 则
则![]()
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调增函数,
上是单调增函数,
故而, ![]() 是
是![]() 在
在![]() 内的唯一零点,即
内的唯一零点,即![]() 是
是![]() 在
在![]() 内的唯一零点.
内的唯一零点.
所以当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上是单调减函数;
上是单调减函数;
当![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上是单调增函数.
上是单调增函数.
(II) ![]()
![]()
![]()
如果![]() 在
在![]() 是凸函数,那么
是凸函数,那么![]() 都有
都有![]()
![]()
令![]() 即得
即得![]()
![]() 当
当![]() 时,
时, ![]() 当
当![]() 时,
时, ![]()
即![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减, 所以
单调递减, 所以![]()
即![]() 又
又![]() 在
在![]() 不是凸函数,所以
不是凸函数,所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(算法流程图)的输出值x为( )
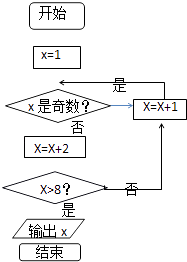
A.13
B.12
C.22
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解2013年某校高三学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为
 ,
,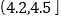 ,… ,
,… , 经过数据处理,得到如右频率分布表:
经过数据处理,得到如右频率分布表: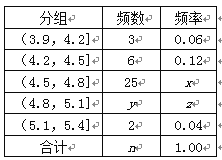
(1)求频率分布表中未知量
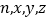 的值;
的值;(2)从样本中视力在
 和
和 的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
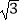 sin(2x+
sin(2x+  ),其中x∈R,下列结论中正确的是( )
),其中x∈R,下列结论中正确的是( )
A.f(x)是最小正周期为π的偶函数
B.f(x)的一条对称轴是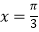
C.f(x)的最大值为2
D.将函数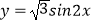 的图象向左平移
的图象向左平移  个单位得到函数f(x)的图象
个单位得到函数f(x)的图象 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
 )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移  个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
A.关于点( ,0)对称
,0)对称
B.关于直线x= 对称
对称
C.关于点(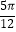 ,0)对称
,0)对称
D.关于直线x=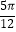 对称
对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的茎叶图是甲、乙两人在4次模拟测试中的成绩,其中一个数字被污损,则甲的平均成绩不超过乙的平均成绩的概率为 .

相关试题

