【题目】已知函数![]() .
.
(1)当![]() 时,若
时,若![]() ,且对任意的
,且对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(2)当![]() 时,求x的取值范围.
时,求x的取值范围.
参考答案:
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)先利用函数的单调性得当x∈[0,1]时,g(x)∈[1,3],f(x)∈[62a,5],再根据已知得到
[1,3][62a,5],解不等式即得解.(2)先化简得![]() ,再对a分类讨论求x的取值范围.
,再对a分类讨论求x的取值范围.
(1)∵g(x)=2x+log2(x+1)在[0,1]上递增,f(x)在[0,1]上递减,
当x∈[0,1]时,g(x)∈[1,3],f(x)∈[62a,5]
∵对任意的x∈[0,1],都存在![]() ∈[0,1],使得f(
∈[0,1],使得f(![]() )=g(x)成立;
)=g(x)成立;
∴[1,3][62a,5]
∴62a1,
即a![]() .
.
(2)![]()
![]()
![]()
当a=0时,x>1
当a≠0时,①当0<a<1时,1<x<![]()
②当a>1时,![]() <x<1
<x<1
③当a=1时,无解
④当a<0时,x<![]() 或x>1
或x>1
综上所述,当a=0时,x的取值范围为![]()
当a≠0时,①当0<a<1时,x的取值范围为![]()
②当a>1时,x的取值范围为![]()
③当a=1时,无解
④当a<0时,x的取值范围为![]()
-
科目: 来源: 题型:
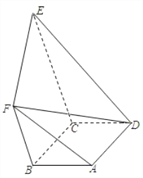
查看答案和解析>>【题目】如图,四边形
 为矩形,四边形
为矩形,四边形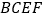 为直角梯形,
为直角梯形, ,
,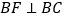 ,
, ,
,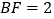 ,
, ,
,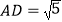 .
.
(1)求证:
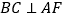 ;
;(2)求证:
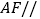 平面
平面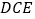 ;
;(3)若二面角
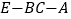 的大小为
的大小为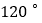 ,求直线
,求直线 与平面
与平面 所成的角.
所成的角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
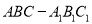 的所有棱长都是
的所有棱长都是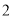 ,
, 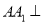 平面
平面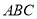 ,
, 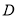 ,
, 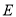 分别是
分别是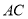 ,
, 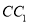 的中点.
的中点.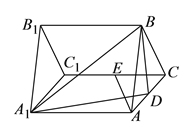
(
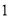 )求证:
)求证: 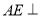 平面
平面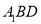 .
.(
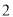 )求二面角
)求二面角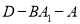 的余弦值.
的余弦值.(
 )求点
)求点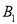 到平面
到平面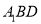 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x3+ax2+bx(x>0)的图像与x轴相切于M(3,0).
(1)求f(x)的解析式;
(2)是否存在两个不等正数s,t(s<t),当x∈[s,t]时,函数f(x)=x3+ax2+bx的值域也是[s,t],若存在,求出所有这样的正数s,t,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
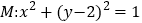 ,
,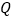 是
是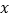 轴上的动点,
轴上的动点, ,
,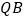 分别切圆
分别切圆 于
于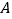 ,
,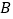 两点.
两点.(
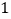 )当
)当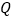 的坐标为
的坐标为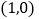 时,求切线
时,求切线 ,
,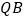 的方程.
的方程.(
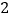 )求四边形
)求四边形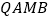 面积的最小值.
面积的最小值.(
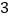 )若
)若 ,求直线
,求直线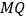 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数
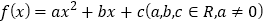 满足条件:
满足条件:(1)当
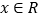 时
时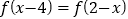 ,且
,且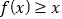 ;
;(2)当
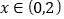 时,
时,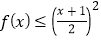 ;
;(3)
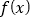 在R上的最小值为0.
在R上的最小值为0.求最大的m(m>1),使得存在
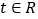 ,只要
,只要 ,就有
,就有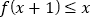
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
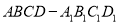 的棱长为1,线段
的棱长为1,线段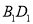 上有两个动点
上有两个动点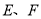 ,则下列结论中正确结论的序号是__________.
,则下列结论中正确结论的序号是__________.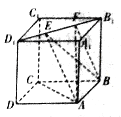
①
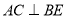 ;
;②直线
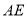 与平面
与平面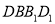 所成角的正弦值为定值
所成角的正弦值为定值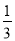 ;
;③当
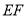 为定值,则三棱锥
为定值,则三棱锥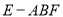 的体积为定值;
的体积为定值;④异面直线
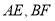 所成的角的余弦值为定值
所成的角的余弦值为定值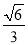 .
.
相关试题

