【题目】设二次函数![]() 满足条件:
满足条件:
(1)当![]() 时
时![]() ,且
,且![]() ;
;
(2)当![]() 时,
时,![]() ;
;
(3)![]() 在R上的最小值为0.
在R上的最小值为0.
求最大的m(m>1),使得存在![]() ,只要
,只要![]() ,就有
,就有![]()
参考答案:
【答案】![]()
【解析】
试题本题主要考查函数的对称性、函数的最值、函数图象、解不等式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.本问利用![]() 先得到函数的对称轴,从而得到a与b的关系,结合③可知函数在对称轴位置取得最小值,结合①和②可得
先得到函数的对称轴,从而得到a与b的关系,结合③可知函数在对称轴位置取得最小值,结合①和②可得![]() ,通过这些方程解出a,b,c的值,从而得到
,通过这些方程解出a,b,c的值,从而得到![]() 解析式,假设存在t,先代入
解析式,假设存在t,先代入![]() ,解不等式得到t的范围,在这个范围内,取
,解不等式得到t的范围,在这个范围内,取![]() 解出m的取值范围,再计算m的最值.
解出m的取值范围,再计算m的最值.
试题解析:∵![]() ∴函数的图象关于
∴函数的图象关于![]() 对称 ∴
对称 ∴![]() ,
,![]() ,
,
由③知当![]() 时,
时,![]() ,即
,即![]() 由①得
由①得![]() ,由②得
,由②得![]() ,
,
∴![]() ,即
,即![]() ,又
,又![]() ∴
∴![]() ,
,
∴![]() ,
,
假设存在![]() ,只要
,只要![]() ,就有
,就有![]() ,
,
取![]() 时,有
时,有![]()
![]()
![]() ,
,
对固定的![]() ,取
,取![]() ,有
,有![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
∴![]() ,
,
当![]() 时,对任意的
时,对任意的![]() ,恒有
,恒有![]()
∴m的最大值为9。
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x3+ax2+bx(x>0)的图像与x轴相切于M(3,0).
(1)求f(x)的解析式;
(2)是否存在两个不等正数s,t(s<t),当x∈[s,t]时,函数f(x)=x3+ax2+bx的值域也是[s,t],若存在,求出所有这样的正数s,t,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
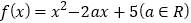 .
.(1)当
 时,若
时,若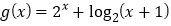 ,且对任意的
,且对任意的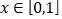 ,都存在
,都存在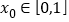 ,使得
,使得 成立,求实数a的取值范围;
成立,求实数a的取值范围;(2)当
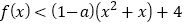 时,求x的取值范围.
时,求x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
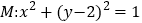 ,
,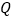 是
是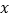 轴上的动点,
轴上的动点, ,
,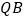 分别切圆
分别切圆 于
于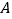 ,
,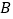 两点.
两点.(
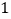 )当
)当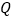 的坐标为
的坐标为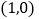 时,求切线
时,求切线 ,
,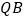 的方程.
的方程.(
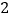 )求四边形
)求四边形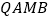 面积的最小值.
面积的最小值.(
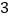 )若
)若 ,求直线
,求直线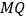 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
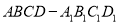 的棱长为1,线段
的棱长为1,线段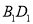 上有两个动点
上有两个动点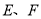 ,则下列结论中正确结论的序号是__________.
,则下列结论中正确结论的序号是__________.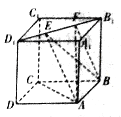
①
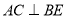 ;
;②直线
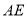 与平面
与平面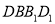 所成角的正弦值为定值
所成角的正弦值为定值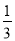 ;
;③当
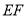 为定值,则三棱锥
为定值,则三棱锥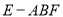 的体积为定值;
的体积为定值;④异面直线
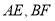 所成的角的余弦值为定值
所成的角的余弦值为定值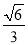 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为2,以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结CF并延长交AB于点E.
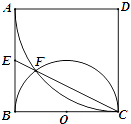
(1)求证:AE=EB;
(2)求EFFC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
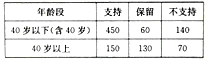
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
相关试题

